题目内容
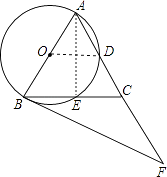
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F. 
(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求 ![]() 的长.
的长.
【答案】
(1)证明:连接AE,
∵AB是⊙O直径,
∴∠AEB=90°,
即AE⊥BC,
∵AB=AC,
∴BE=CE
(2)解:∵∠BAC=54°,AB=AC,
∴∠ABC=63°,
∵BF是⊙O切线,
∴∠ABF=90°,
∴∠CBF=∠ABF﹣∠ABC=27°
(3)解:连接OD,
∵OA=OD,∠BAC=54°,
∴∠AOD=72°,
∵AB=6,
∴OA=3,
∴弧AD的长是 ![]() =
= ![]() .
.
【解析】(1)连接AE,求出AE⊥BC,根据等腰三角形性质求出即可;(2)求出∠ABC,求出∠ABF,即可求出答案;(3)求出∠AOD度数,求出半径,即可求出答案.
【考点精析】本题主要考查了圆周角定理和切线的性质定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

 七彩题卡口算应用一点通系列答案
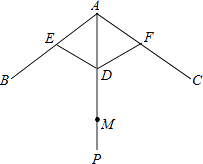
七彩题卡口算应用一点通系列答案【题目】如图,伞不论张开还是收紧,伞柄AP始终平分同一平面内两条伞架所成的角∠BAC,当伞收紧时,结点D与点M重合,且点A、E、D在同一条直线上,已知部分伞架的长度如下:单位:cm
伞架 | DE | DF | AE | AF | AB | AC |
长度 | 36 | 36 | 36 | 36 | 86 | 86 |
(1)求AM的长.
(2)当∠BAC=104°时,求AD的长(精确到1cm). 备用数据:sin52°=0.788,cos52°=0.6157,tan52°=1.2799.




