题目内容
【题目】在同一平面内,已知线段AO=2,⊙A的半径为1,将⊙A绕点O按逆时针方向旋转60°得到的像为⊙B,则⊙A与⊙B的位置关系为 .
【答案】外切
【解析】解:∵⊙A绕点O按逆时针方向旋转60°得到的⊙B, ∴△OAB为等边三角形,
∴AB=OA=2,
∵⊙A、⊙B的半径都为1,
∴AB等于两圆半径之和,
∴⊙A与⊙B外切.
所以答案是外切.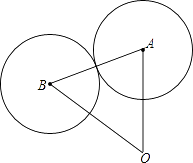
【考点精析】关于本题考查的圆与圆的位置关系和旋转的性质,需要了解两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.

练习册系列答案
相关题目