Question

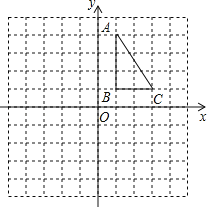
【题目】如图，直线分别与轴轴交于点D、A、CD⊥轴，且CD=4，点P在线段OD上运动.

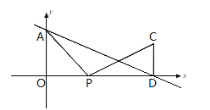
（1）求出点A和点D的坐标；

（2）是否存在这样的点P使△AOP与△PCD相似，若存在，求出点P的坐标，若不存在，说明理由.

Answer 1

【答案】（1）A（0，6），D（14，0）;（2）P（12，0）或（2，0）或（8.4，0）

【解析】

（1）分别令x=0，y=0，即可求出A、D的坐标；

（2）设P点坐标为（a，0），用a表示出PD，分别讨论△AOP∽△PDC，△AOP∽△CDP，利用对应边成比例建立方程求解.

解：（1）当x=0时，y=6，所以A点坐标（0,6）

当y=0时，，解得，所以D点坐标（14,0）

故答案为A（0，6），D（14，0）.

（2）设P点坐标为（a，0），则OP=a，PD=14-a，

当△AOP∽△PDC时，

，即，

解得，，

所以P点坐标为（12，0）或（2，0），

当△AOP∽△CDP时，

，即，

解得

所以P点坐标为（8.4,0）

综上可得：P（12，0）或（2，0）或（8.4，0）.