题目内容
【题目】给出如下定义：对于⊙O的弦MN和⊙O外一点P（M，O，N三点不共线，且点P，O在直线MN的异侧），当∠MPN+∠MON＝180°时，则称点P是线段MN关于点O的关联点．图1是点P为线段MN关于点O的关联点的示意图．
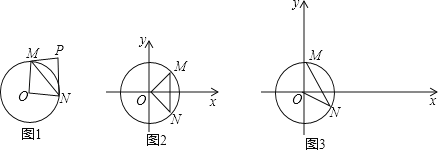
在平面直角坐标系xOy中，⊙O的半径为1．
（1）如图2，已知M（
，），N（，﹣），在A（1，0），B（1，1），C（
，0）三点中，是线段MN关于点O的关联点的是 ；
（2）如图3，M（0，1），N（
，﹣
），点D是线段MN关于点O的关联点．
①∠MDN的大小为 ；
②在第一象限内有一点E（
m，m），点E是线段MN关于点O的关联点，判断△MNE的形状，并直接写出点E的坐标；
③点F在直线y＝﹣
x+2上，当∠MFN≥∠MDN时，求点F的横坐标x的取值范围．
【答案】（1）C；（2）①60；②E（
，1）；③点F的横坐标x的取值范围
≤xF≤．
【解析】
（1）由题意线段MN关于点O的关联点的是以线段MN的中点为圆心，
为半径的圆上，所以点C满足条件；
（2）①如图3-1中，作NH⊥x轴于H．求出∠MON的大小即可解决问题；
②如图3-2中，结论：△MNE是等边三角形．由∠MON+∠MEN=180°，推出M、O、N、E四点共圆，可得∠MNE=∠MOE=60°，由此即可解决问题；
③如图3-3中，由②可知，△MNE是等边三角形，作△MNE的外接圆⊙O′，首先证明点E在直线y=-
x+2上，设直线交⊙O′于E、F，可得F（，
），观察图形即可解决问题；
（1）由题意线段MN关于点O的关联点的是以线段MN的中点为圆心，为半径的圆上，所以点C满足条件，
故答案为C．
（2）①如图3-1中，作NH⊥x轴于H．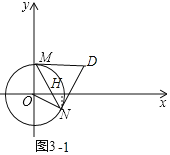
∵N（，-
），
∴tan∠NOH=，
∴∠NOH=30°，
∠MON=90°+30°=120°，
∵点D是线段MN关于点O的关联点，
∴∠MDN+∠MON=180°，
∴∠MDN=60°．
故答案为60°．
②如图3-2中，结论：△MNE是等边三角形．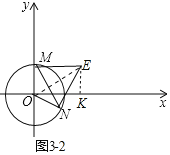
理由：作EK⊥x轴于K．
∵E（，1），
∴tan∠EOK=，
∴∠EOK=30°，
∴∠MOE=60°，
∵∠MON+∠MEN=180°，
∴M、O、N、E四点共圆，
∴∠MNE=∠MOE=60°，
∵∠MEN=60°，
∴∠MEN=∠MNE=∠NME=60°，
∴△MNE是等边三角形．
③如图3-3中，由②可知，△MNE是等边三角形，作△MNE的外接圆⊙O′，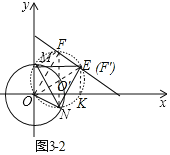
易知E（，1），
∴点E在直线y=-x+2上，设直线交⊙O′于E、F，可得F（，），
观察图象可知满足条件的点F的横坐标x的取值范围≤xF≤．
