Question

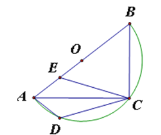
【题目】如图，在Rt△ABC中，∠ACB=90°，以AB为直径作半圆．点D在弧上（不与A，C重合），点E在AB上，且点D.E关于AC对称. 给出下列结论：①若∠ACE=20°，则∠BAC=25°；②若BC=3，AC=4，则；给出下列判断，正确的是（ ）

A.①②都对B.①②都错C.①对②错D.①错②对

Answer 1

【答案】D

【解析】

①根据圆内接四边形对角线互补的性质求出∠B，即可求出∠BAC=35°；

②作辅助线，然后利用相似的性质求解即可.

解：∵点D.E关于AC对称

∴∠AEC=∠ADC

根据∠ADC+∠B=180°，∠ACE=20°

∴∠BEC=180°-∠AEC=∠B，∠BCE=70°

∴∠B=55°

∴∠BAC=35°,故①错误；

②∵BC=3，AC=4

∴AB=5

作CF⊥AD

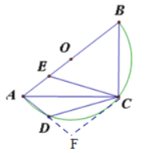
则ABC~DCF

∴

∴

∵∠CDF=∠B

∴

∴

∴

故②正确.

故选D.