题目内容
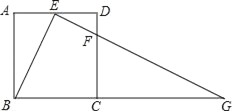
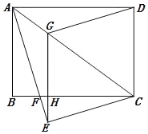
【题目】如图,把矩形ABCD沿AC折叠,使点D与点E重合,AE交BC于点F,过点E作EG∥CD交AC于点G,交CF于点H,连接DG.
(1)求证:四边形ECDG是菱形;
(2)若DG=6,AG=![]() ,求EH的值.
,求EH的值.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据折叠的性质,邻边相等的平行四边形为菱形证得结论;
(2)如图,连接![]() 交
交![]() 于点
于点![]() ,构造相似三角形
,构造相似三角形![]() ,由该相似三角形的对应边成比例求得
,由该相似三角形的对应边成比例求得![]() ,可求
,可求![]() 的长,
的长,![]() 的长,通过证明
的长,通过证明![]() 可得
可得![]() 的长,即可求
的长,即可求![]() 的值.
的值.
解:(1)由折叠可知DC=EC,∠DCG=∠ECG.
∵EG∥CD,
∴∠DCG=∠EGC,
∴∠EGC=∠ECG,
∴EG=EC,
∴EG=DC,且EG∥CD
∴四边形ECDG是平行四边形.
∵EG=EC,
∴平行四边形ECDG是菱形
(2)如图,连接ED交AC于点O,
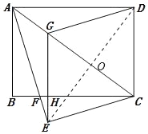
∵四边形ECDG是菱形,
∴ED⊥AC,![]() ,CD=GE=6=DG,
,CD=GE=6=DG,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴△DCO∽△ACD,
∴![]() ,
,
∴DC2=OCAC,
设OC=x,则CG=2x,![]() ,
,
∴36=x(2x+![]() ),
),
解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() ,
,![]() ,
,
∵EG∥CD,CD⊥BC,
∴EG⊥BC,
∴∠DAC=∠ACB,且∠GHC=∠ADC=90°,
∴△ADC∽△CHG,
∴![]() ,
,
∴GH=![]() ,
,
∵EH=EG﹣GH,
∴EH=6﹣![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.