题目内容
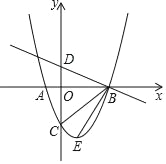
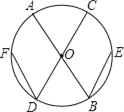
【题目】如图，AB、CD是⊙O的直径，DF、BE是弦，且DF＝BE，求证：∠D＝∠B．
【答案】略
【解析】
根据在同圆中等弦对的弧相等，AB、CD是⊙O的直径，则弧CFD=弧AEB，由FD=EB，得，弧FD=弧EB，由等量减去等量仍是等量得：弧CFD-弧FD=弧AEB-弧EB，即弧FC=弧AE，由等弧对的圆周角相等，得∠D=∠B．
方法（一）
证明：∵AB、CD是⊙O的直径，
∴弧CFD=弧AEB．
∵FD=EB，
∴弧FD=弧EB．
∴弧CFD-弧FD=弧AEB-弧EB．
即弧FC=弧AE．
∴∠D=∠B．
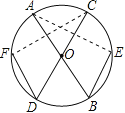
方法（二）
证明：如图，连接CF，AE．
∵AB、CD是⊙O的直径，
∴∠F=∠E=90°（直径所对的圆周角是直角）．
∵AB=CD，DF=BE，
∴Rt△DFC≌Rt△BEA（HL）．
∴∠D=∠B．
练习册系列答案
阅读快车系列答案
相关题目
