Question

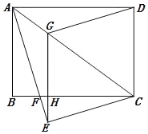
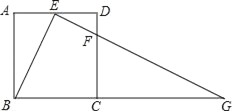
【题目】如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE＝ED，DF：DC＝1：4，连接EF并延长交BC的延长线于点G．

（1）求证：△ABE∽△DEF；

（2）若正方形的边长为10，求BG的长．

Answer 1

【答案】（1）见解析；（2）25

【解析】

（1）由题意可得AE=DE=AD=AB，DF=CD=AD，即可证△ABE∽△DEF；
（2）由题意可得AE=DE=5，DF=，CF=，由相似三角形的性质可得CG=15，即可求BG的长．

证明：∵四边形ABCD是正方形，

∴∠A＝∠D＝90°，AB＝AD＝CD，

∵AE＝ED，DF：DC＝1：4，

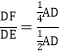∴AE＝DE＝AD＝AB，DF＝CD＝AD，

∵，＝

∴=，且∠A＝∠D，

∴△ABE∽△DEF

（2）∵CB＝AD＝CD＝10，

∴AE＝DE＝5，DF＝，CF＝

∵AD∥BC

∴△DEF∽△CGF

∴=，

∴CG＝15

∴BG＝BC+CG＝10+15＝25