题目内容
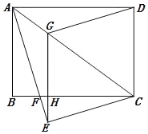
【题目】如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2﹣CF2取最大值时,求tan∠DCF的值.

【答案】解:(1)∵α=60°,BC=10,∴sinα=![]() ,即sin60°=
,即sin60°=![]() ,解得CE=
,解得CE=![]() 。
。
(2)①存在k=3,使得∠EFD=k∠AEF。理由如下:
连接CF并延长交BA的延长线于点G,

∵F为AD的中点,∴AF=FD。
在平行四边形ABCD中,AB∥CD,∴∠G=∠DCF。
在△AFG和△CFD中,
∵∠G=∠DCF, ∠G=∠DCF,AF=FD,
∴△AFG≌△CFD(AAS)。∴CF=GF,AG=CD。
∵CE⊥AB,∴EF=GF。∴∠AEF=∠G。
∵AB=5,BC=10,点F是AD的中点,∴AG=5,AF=![]() AD=
AD=![]() BC=5。∴AG=AF。
BC=5。∴AG=AF。
∴∠AFG=∠G。
在△AFG中,∠EFC=∠AEF+∠G=2∠AEF,
又∵∠CFD=∠AFG,∴∠CFD=∠AEF。
∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF,
因此,存在正整数k=3,使得∠EFD=3∠AEF。
②设BE=x,∵AG=CD=AB=5,∴EG=AE+AG=5﹣x+5=10﹣x,
在Rt△BCE中,CE2=BC2﹣BE2=100﹣x2。
在Rt△CEG中,CG2=EG2+CE2=(10﹣x)2+100﹣x2=200﹣20x。
∵CF=GF(①中已证),∴CF2=(![]() CG)2=
CG)2=![]() CG2=
CG2=![]() (200﹣20x)=50﹣5x。
(200﹣20x)=50﹣5x。
∴CE2﹣CF2=100﹣x2﹣50+5x=﹣x2+5x+50=﹣(x﹣![]() )2+50+
)2+50+![]() 。
。
∴当x=![]() ,即点E是AB的中点时,CE2﹣CF2取最大值。
,即点E是AB的中点时,CE2﹣CF2取最大值。
此时,EG=10﹣x=10﹣![]() ,CE=
,CE=![]() ,
,
∴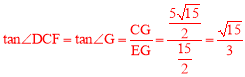 。
。
【解析】锐角三角函数定义,特殊角的三角函数值,平行四边形的性质,对顶角的性质,全等三角形的判定和性质,直角三角形斜边上的中线性质,等腰三角形的性质,二次函数的最值,勾股定理。
(1)利用60°角的正弦值列式计算即可得解。
(2)①连接CF并延长交BA的延长线于点G,利用“角边角”证明△AFG和△CFD全等,根据全等三角形对应边相等可得CF=GF,AG=CD,再利用直角三角形斜边上的中线等于斜边的一半可得EF=GF,再根据AB、BC的长度可得AG=AF,然后利用等边对等角的性质可得∠AEF=∠G=∠AFG,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G,然后推出∠EFD=3∠AEF,从而得解。
②设BE=x,在Rt△BCE中,利用勾股定理表示出CE2,表示出EG的长度,在Rt△CEG中,利用勾股定理表示出CG2,从而得到CF2,然后相减并整理,再根据二次函数的最值问题解答。

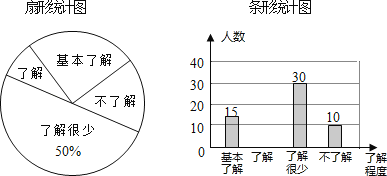
【题目】某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表,请根据图表中提供的信息解答下列问题:
AQI指数 | 质量等级 | 天数(天) |
0-50 | 优 | m |
51-100 | 良 | 44 |
101-150 | 轻度污染 | n |
151-200 | 中度污染 | 4 |
201-300 | 重度污染 | 2 |
300以上 | 严重污染 | 2 |

(1)统计表中m= ,n= ,扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少?