题目内容
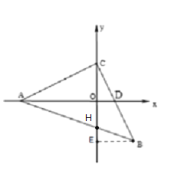
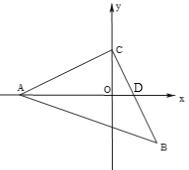
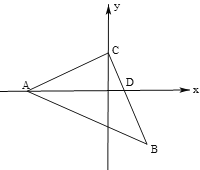
【题目】在平面直角坐标系中,三角形△ABC为等腰直角三角形,AC=BC,BC交x轴于点D.
(1)若A(-4,0),C(0,2),求点B的坐标;
(2)若∠EDB=∠ADC,问∠ADE与∠CAD满足怎样的关系?并证明.
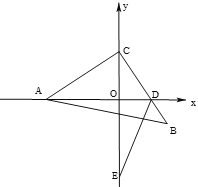
(3)若AD平分∠BAC,A(-4,0),D(m,0),B的纵坐标为n,试探究m、n之间满足怎样的关系?
【答案】(1)(2,-2);(2)∠ADE=2∠CAD;(3)(4+n)2=4m
【解析】
(1)作BE垂直于y轴于点E,证明△ACO≌△CBE,再通过A,C的坐标求出B点坐标即可;(2)∠ADC为△ADB的外角,则∠ADC=∠B+∠DAB,∠AFD是△DFB的外角,∠AFD=∠B+∠EDB,再通过角度转换得到∠ADE与∠CAD的关系即可(3)作BE垂直于y轴于点E,证明△ACO≌△CBE,再由AD为角平分线,则△COD∽△AOH,通过相似比列出m,n的关系式即可.
(1)作BE垂直于y轴于点E,
∵∠ACO+∠ECB=90°,∠ACO+∠CAO=90°,
∴∠CAO=∠BCE,
在△ACO和△CBE中
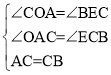
∴△ACO≌△CBE(AAS)
∵A(-4,0),C(0,2),
∴BE=CO=2,CE=AO=4,
∴OE=2,
∴点B的坐标为(2,-2);
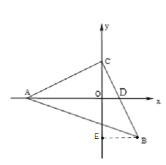
(2)AB,ED的交点记为F,
∠ADC为△ADB的外角,
则∠ADC=∠B+∠DAB,
∵∠ADC=∠EDB,
∴∠EDB=∠B+∠DAB,
∵∠AFD是△DFB的外角,
∴∠AFD=∠B+∠EDB,
∵△ABC为等腰直角三角形,
∴∠B=∠CAB=45°,
∴∠AFD=90°+∠FAD,
∴∠ADF=180°-(90°+∠FAD)-∠FAD=90°-2∠FAD,
∠FAD=45°-∠CAD,
∴∠ADE=90°-2(45°-∠CAD),
∴∠ADE=2∠CAD;
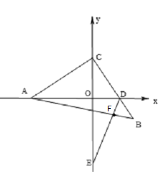
(3)作BE垂直于y轴于点E,AB与y轴交于点H,
∵∠ACO+∠ECB=90°,∠ACO+∠CAO=90°,
∴∠CAO=∠BCE,
在△ACO和△CBE中
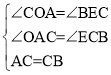
∴△ACO≌△CBE(AAS)
∵A(-4,0),D(m,0),B的纵坐标为n,
∴CE=AO=4,OE=-n,CO=4+n,
∵AD平分∠CAB,
则AH=AC,CO=OH,
则△COD∽△AOH,
![]()
则(4+n)2=4m