题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,且BC=4,则△ABC 的面积为_____________.

【答案】![]()
【解析】由CM为Rt△ABC斜边AB上的中线,根据直角三角形斜边上的中线性质得CM=MB=AM,再根据折叠的性质得到MD=MA,∠DMC=∠AMC,则MD=MC,由于CD⊥MB于H,
根据等腰三角形的性质有MH平分∠DMC,即∠BMC=∠BMD,可得∠DMC=2∠BMC,∠AMC=2∠BMC,利用平角的定义可计算出∠BMC=60°,则△BMC为等边三角形,易得
∠B=60°,∠A=30°,所以AC=![]() BC=4
BC=4![]() ,然后根据三角形面积公式进行计算.
,然后根据三角形面积公式进行计算.
如图,
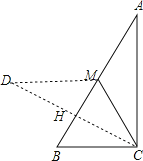
∵CM为Rt△ABC斜边AB上的中线,
∴CM=MB=AM,
∵沿△ABC的中线CM将△CMA折叠,点A落在点D处,
∴MD=MA,∠DMC=∠AMC,
∴MD=MC,
∵CD⊥MB于H,
∴MH平分∠DMC,即∠BMC=∠BMD,
∴∠DMC=2∠BMC,
∴∠AMC=2∠BMC,
∵∠BMC+∠AMC=180°,
∴∠BMC=60°,
∴△BMC为等边三角形,
∴∠B=60°,
∴∠A=30°,
∴AC=![]() BC=4
BC=4![]() ,
,
∴S△ABC=![]() ACBC=
ACBC=![]() ×4
×4![]() ×4=8
×4=8![]() .
.
故答案为8![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目