题目内容
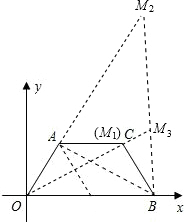
如图,在平面直角坐标系中,等腰梯形AOBC的四个顶点坐标分别为A(2,2
),O(0,0),B(8 ,0),C(6,2
,0),C(6,2
).
(1)求等腰梯形AOBC的面积;
(2)试说明点A在以OB的中点D为圆心,OB为直径的圆上;
(3)在第一象限内确定点M,使△MOB与△AOB相似,求出所有符合条件的点M的坐标.
| 3 |
 ,0),C(6,2
,0),C(6,2| 3 |
(1)求等腰梯形AOBC的面积;
(2)试说明点A在以OB的中点D为圆心,OB为直径的圆上;
(3)在第一象限内确定点M,使△MOB与△AOB相似,求出所有符合条件的点M的坐标.
(1)∵A(2,2
),B(8,0),C(6,2
),梯形AOBC是等腰梯形,
∴S梯形=
(上底+下底)×高=
×(4+8)×2
=12
.
(2)连接AB,那么AB2=62+(2
)2=48,
根据A,B的坐标可知:OA2=22+(2
)2=16,OB2=82=64,
∴OB2=AB2+OA2.
因此三角形OAB是直角三角形,且OB为斜边.
∴OB=2AD,因此点A在圆D上.
(3)点M1位于点C上时,△OM1B与△OAB相似此时点M1的坐标为M1(6,2
).
过B点作OB的垂线交OA的延长线于M2.
△OM2B与△OAB相似,此时点M2的坐标为M2(8,8
).
过B点作OB的垂线交OC的延长线于M3.
△OM3B与△OAB相似此时点M3的坐标为M3(8,
).
| 3 |
| 3 |
∴S梯形=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)连接AB,那么AB2=62+(2
| 3 |
根据A,B的坐标可知:OA2=22+(2
| 3 |
∴OB2=AB2+OA2.
因此三角形OAB是直角三角形,且OB为斜边.
∴OB=2AD,因此点A在圆D上.
(3)点M1位于点C上时,△OM1B与△OAB相似此时点M1的坐标为M1(6,2
| 3 |
过B点作OB的垂线交OA的延长线于M2.
△OM2B与△OAB相似,此时点M2的坐标为M2(8,8
| 3 |
过B点作OB的垂线交OC的延长线于M3.
△OM3B与△OAB相似此时点M3的坐标为M3(8,
8
| ||
| 3 |


练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目