��Ŀ����
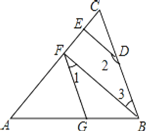
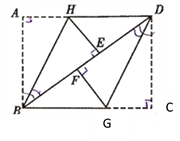
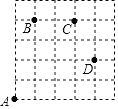
����Ŀ����ͼ1���ı���ABCD�������Σ�G��CD���ϵ�һ�����㣨��G��C��D���غϣ�����CGΪһ����������ABCD����������CEFG������BG��DE��
��1���ٲ���ͼ1���߶�BG���߶�DE�ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ������֤����
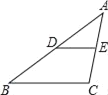
�ڽ�ͼ1�е�������CEFG���ŵ�C��˳ʱ�뷽����ת����Ƕ������õ���ͼ2���Σ�����ͨ���۲졢�����ȷ����жϢ��еõ��Ľ����Ƿ���Ȼ��������֤������жϣ�
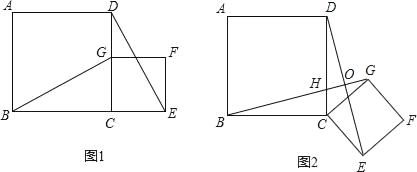
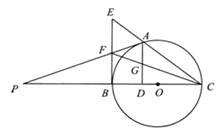
��2����ԭ���������θ�Ϊ���Σ���ͼ3��4������AB=a��BC=b��CE=ka��CG=kb ��a��b��k��0�����ڣ�1������еõ��Ľ�����Щ��������Щ������������������ͼ4Ϊ����Ҫ˵�����ɣ�
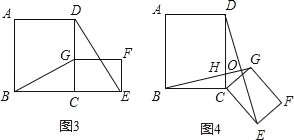
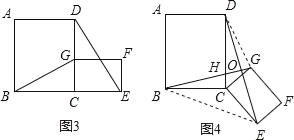
��3���ڵڣ�2����ͼ4�У�����DG��BE����a=3��b=2��k=![]() ����BE2+DG2��ֵ��
����BE2+DG2��ֵ��
���𰸡���1����BG��DE��BG=DE����BG��DE��֤������������2��BG��DE��֤������������3��16.25��
����������������1���ٸ��������ε����ʣ���Ȼ������BCG˳ʱ����ת90�㼴�ɵõ�������DCE���Ӷ��ж�����ֱ��֮��Ĺ�ϵ��
�ڽ�������ε����ʣ�����SAS��Ȼ�ܹ��ж���BCG�ա�DCE���Ӷ�֤�����ۣ�
��2������������Ӧ�ߵı���ȣ��Ҽн���ȿ����ж������������������ƣ��Ӷ����Եõ���1���е�λ�ù�ϵ��Ȼ������
��3������BE��DG�����ݹ��ɶ������ɰ�BE2+DG2ת��Ϊ�������εij�����ƽ���ͣ�
��⣺��1����BG��DE��BG=DE��
�ڡ��ı���ABCD���ı���CEFG�������Σ�
��BC=DC��CG=CE����BCD=��ECG=90�㣬
���BCG=��DCE��
���BCG�ա�DCE��
��BG=DE����CBG=��CDE��
�֡ߡ�CBG+��BHC=90�㣬
���CDE+��DHG=90�㣬
��BG��DE��
��2����AB=a��BC=b��CE=ka��CG=kb��
��![]() ��
��
�֡ߡ�BCG=��DCE��
���BCG�ס�DCE��
���CBG=��CDE��
�֡ߡ�CBG+��BHC=90�㣬
���CDE+��DHG=90�㣬
��BG��DE��
��3������BE��DG��
�������⣬��AB=3��BC=2��CE=1.5��CG=1��
��BG��DE����BCD=��ECG=90��
��BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�