题目内容
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为![]() 的是( )
的是( )
A. 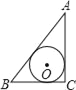 B.
B. 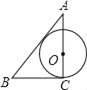 C.
C. 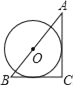 D.
D. 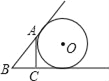
【答案】C
【解析】解:设⊙O的半径为r.
A.∵⊙O是△ABC内切圆,∴S△ABC=![]() (a+b+c)r=
(a+b+c)r=![]() ab,∴r=
ab,∴r=![]() ;
;
B.如图,连接OD,则OD=OC=r,OA=b﹣r.∵AD是⊙O的切线,∴OD⊥AB,即∠AOD=∠C=90°,∴△ADO∽△ACB,∴OA:AB=OD:BC,即(b﹣r):c=r:a,解得:r=![]() ;
;
C.连接OE,OD.∵AC与BC是⊙O的切线,∴OE⊥BC,OD⊥AC,∴∠OEB=∠ODC=∠C=90°,∴四边形ODCE是矩形.∵OD=OE,∴矩形ODCE是正方形,∴EC=OD=r,OE∥AC,∴OE:AC=BE:BC,∴r:b=(a﹣r):a,∴r=![]() ;
;
D.设AC、BA、BC与⊙O的切点分别为D、F、E,连接OD、OE.
∵AC、BE是⊙O的切线,∴∠ODC=∠OEC=∠DCE=90°,∴四边形ODCE是矩形.
∵OD=OE,∴矩形ODCE是正方形,即OE=OD=CD=r,则AD=AF=b﹣r.
连接OB,OF,由勾股定理得:BF2=OB2﹣OF2,BE2=OB2﹣OE2.∵OB=OB,OF=OE,∴BF=BE,则BA+AF=BC+CE,c+b﹣r=a+r,即r=![]() .
.
故选C.
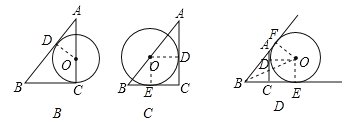

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目