题目内容
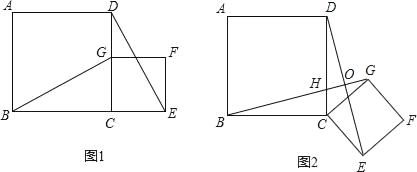
【题目】如图,∠AGF=∠ABC,∠ 1+∠ 2=180°.
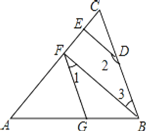
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠CDE=30°,求∠AFG的度数.
【答案】(1)BF∥DE,理由解析;(2)60°
【解析】
(1)先结合图形猜想DE∥BF,由平行线的判定可知只需证∠2+∠3=180°,根据平行线的性质结合已知条件即可求证;
(2)根据补角的定义及已知∠ 1+∠ 2=180°,可求得∠1 =30°,再根据余角的定义即可求得答案.
(1)BF与DE的位置关系是:BF∥DE.
理由:∵∠AGF=∠ABC,
∴BC∥GF(同位角相等,两直线平行),
∴∠1=∠3;
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE;
(2)∵BF∥DE,BF⊥AC,
∴DE⊥AC,
∵∠CDE=30°,∠CDE +∠2=180°
∵∠1+∠2=180°,
∴∠1=∠CDE=30°,
∴∠AFG=90°-30°=60°.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目