Question

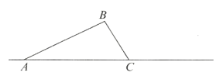
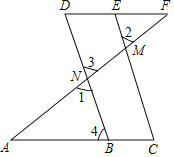
【题目】如图，证明定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．

已知：点D、E分别是△ABC的边AB、AC的中点．

求证：DE∥BC，DE＝BC．

Answer 1

【答案】见解析

【解析】

延长DE至F，使EF=DE，连接CF，通过证明△ADE≌△CFE和证明四边形BCFD是平行四边形即可证明三角形的中位线平行于三角形的第三边并且等于第三边的一半．

证明：延长DE至F，使EF＝DE，连接CF

∵E是AC中点，

∴AE＝CE，

在△ADE和△CFE中，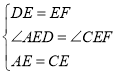

∴△ADE≌△CFE（SAS），

∴AD＝CF，∠ADE＝∠F

∴BD∥CF，

∵AD＝BD，

∴BD＝CF

∴四边形BCFD是平行四边形（一组对边平行且相等的四边形是平行四边形）

∴DF∥BC，DF＝BC，

∴DE∥CB，DE＝BC．