题目内容
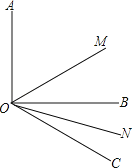
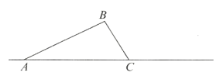
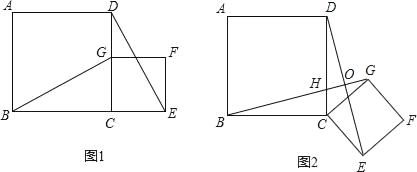
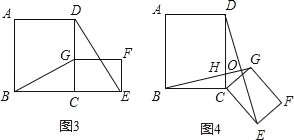
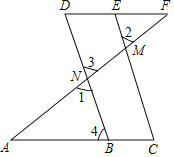
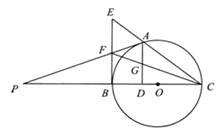
【题目】如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
(1)求证:BF=EF:
(2)求证:PA是⊙O的切线;
(3)若FG=BF,且⊙O的半径长为3![]() ,求BD的长度.
,求BD的长度.
【答案】(1)证明见解析;(2) 证明见解析;(3)2![]()
【解析】分析:(1)利用平行线截三角形得相似三角形,得△BFC∽△DGC且△FEC∽△GAC,得到对应线段成比例,再结合已知条件可得BF=EF;
(2)利用直角三角形斜边上的中线的性质和等边对等角,得到∠FAO=∠EBO,结合BE是圆的切线,得到PA⊥OA,从而得到PA是圆O的切线;
(3)点F作FH⊥AD于点H,根据前两问的结论,利用三角形的相似性质即可以求出BD的长度.
详解:证明:(1)∵BC是圆O的直径,BE是圆O的切线,
∴EB⊥BC.
又∵AD⊥BC,
∴AD∥BE.
∴△BFC∽△DGC,△FEC∽△GAC,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵G是AD的中点,
∴DG=AG,
∴BF=EF;
(2)连接AO,AB.

∵BC是圆O的直径,
∴∠BAC=90°,
由(1)得:在Rt△BAE中,F是斜边BE的中点,
∴AF=FB=EF,可得∠FBA=∠FAB,
又∵OA=OB,
∴∠ABO=∠BAO,
∵BE是圆O的切线,
∴∠EBO=90°,
∴∠FBA+∠ABO=90°,
∴∠FAB+∠BAO=90°,
即∠FAO=90°,
∴PA⊥OA,
∴PA是圆O的切线;
(3)过点F作FH⊥AD于点H,
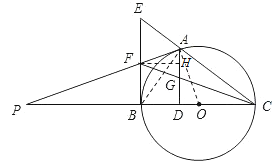
∵BD⊥AD,FH⊥AD,
∴FH∥BC,
由(2),知∠FBA=∠BAF,
∴BF=AF.
∵BF=FG,
∴AF=FG,
∴△AFG是等腰三角形.
∵FH⊥AD,
∴AH=GH,
∵DG=AG,
∴DG=2HG.
即![]() ,
,
∵FH∥BD,BF∥AD,∠FBD=90°,
∴四边形BDHF是矩形,
∴BD=FH,
∵FH∥BC
∴△HFG∽△DCG,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∵O的半径长为3![]() ,
,
∴BC=6![]() ,
,
∴BD=![]() =2
=2![]() .
.

【题目】某校八年级(1)班积极响应校团委的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐图书400册.特别值得一提的是李保、王刚两位同学在父母的支持下各捐献了90册图书.班长统计了全班捐书情况如下表(被粗心的马小虎用墨水污染了一部分):
册数 | 4 | 5 | 6 | 7 | 8 | 90 |
人数 | 6 | 8 | 15 | 2 |
(1)分别求出该班级捐献7册图书和8册图书的人数;
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪个统计量不能反映该班同学捐书册数的一般状况,说明理由.