Question

【题目】某地政府计划为农户购买农机设备提供补贴．其中购买Ⅰ型、Ⅱ型设备农民所投资的金额与政府补贴的额度存在下表所示的函数对应关系．

型号 金额	Ⅰ型设备		Ⅱ型设备
投资金额x（万元）	x	5	x	2	4
补贴金额y（万元）	y1＝kx（k≠0）	2	y2＝ax2+bx（a≠0）	2.8	4

（1）分别求y1和y2的函数解析式；

（2）有一农户共投资10万元购买Ⅰ型、Ⅱ型两种设备，两种设备的投资均为整数万元，要想获得最大补贴金额，应该如何购买？能获得的最大补贴金额为多少？

Answer 1

【答案】（1）y1的解析式为：y1＝x，y2的函数解析式为：y2＝﹣x2+x；（2）以投资Ⅰ型设备7万元，Ⅱ型设备3万元；或投资Ⅰ型设备6万元，Ⅱ型设备4万元，获得最大补贴金额，最大补贴金额为万元．

【解析】

（1）根据待定系数法，分别代值解方程即得；

（2）先根据列出二次函数解析式，再将解析式化为顶点式即得．

解：（1）设购买Ⅰ型设备补贴的金额的解析式为：，购买Ⅱ型设备补贴的金额的解析式为．

由题意，得：2=5k，且，解得：k=，且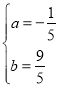

∴y1的解析式为：y1=x，y2的解析式为：y2=-x2+x．

（2）设投资Ⅱ型设备a万元，Ⅰ型设备（10﹣a）万元，补贴金额为W万元：

由题意，得：

∵a为整数

∴当a＝3或4时，W的最大值=

∴投资Ⅰ型设备7万元，Ⅱ型设备3万元；或投资Ⅰ型设备6万元，Ⅱ型设备4万元，获得最大补贴金额，最大补贴金额为万元．