Question

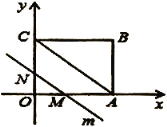
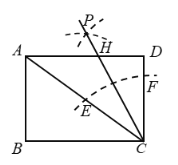
【题目】问题：如图1，在中，，点是射线上任意一点，是等边三角形，且点在的内部，连接．探究线段与之间的数量关系．

请你完成下列探究过程：

先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．

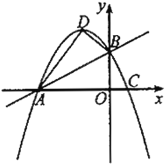
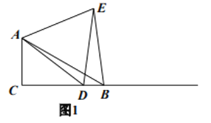
当点与点重合时(如图2)，请你补全图形．由的度数为_______________，点落在_______________，容易得出与之间的数量关系为_______________

当是的平分线时，判断与之间的数量关系并证明

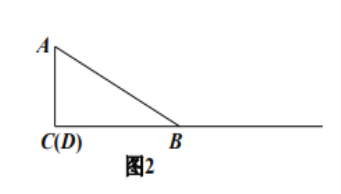
当点在如图3的位置时，请你画出图形，研究三点是否在以为圆心的同一个圆上，写出你的猜想并加以证明．

Answer 1

【答案】（1）60°；AB的中点处；BE=DE；（2）BE=DE，理由见解析；（3）A、B、D在以E为圆心的同一个圆上，画图和理由见解析

【解析】

（1）根据题意画出图形，由直角三角形及等边三角形的性质即可得出结论；
（2）画出图形，根据题意证明AD=BD，再由△ADE是等边三角形，得出∠BDE=60°，即△BDE为等边三角形，可得结论；

（3）根据题意画出图形，猜想：BE=DE，取AB的中点F，连接EF，由∠ACB=90°，∠ABC=30°，可知∠1=60°，CF=AF=AB，故△ACF是等边三角形，再由△ADE是等边三角形可得出∠CAD=∠FAE，由全等三角形的判定定理可知△ACD≌△AFE，故∠ACD=∠AFE=90°．由F是AB的中点，可知EF是AB的垂直平分线，进而可得出△ADE是等边三角形，故DE=AE，BE=DE，可得点E在BD的垂直平分线上，即可证明.

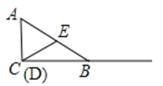
解：（1）如图，
∵∠C=90°，∠ABC=30°，
∴∠BAC=60°，
∵△ADE是等边三角形，
∴AE=CE，
∴点E落在AB的中点处；
∴AE=CE=BE=DE，
故答案为：60°；AB的中点处；BE=DE；

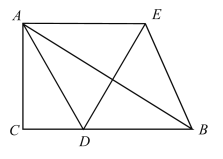
（2）BE=DE，

∵AD平分∠BAC，∠BAC=60°，

∴∠BAD=30°=∠ABC=∠CAD，

∴AD=BD，

∵△ADE是等边三角形，

∴DE=AD，

∴DE=DB，

∵∠C=90°，

∴∠ADC=∠ADE=60°，

∴∠BDE=60°，

∴△BDE为等边三角形，

∴BE=DE；

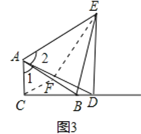
（3）如图为所画图形，

猜想：A、B、D在以E为圆心的同一个圆上，

理由是：设AB中点为F，连接CF，EF，

∵∠ACB=90°，∠ABC=30°，
∴∠1=60°，CF=AF=AB，
∴△ACF是等边三角形．
∴AC=AF，
∵△ADE是等边三角形，
∴∠2=60°，AD=AE，
∴∠1=∠2，
∴∠1+∠BAD=∠2+∠BAD，
即∠CAD=∠FAE，

在△ACD和△AFE中，

，
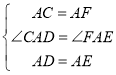∴△ACD≌△AFE（SAS），
∴∠ACD=∠AFE=90°，
∵F是AB的中点，
∴EF是AB的垂直平分线，
∴BE=AE，
∵△ADE是等边三角形，
∴DE=AE，
∴BE=DE，

∴点E在BD的垂直平分线上，

∴A、B、D在以点E为圆心的同一个圆上.