题目内容
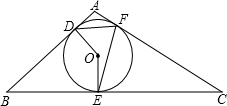
Rt△ABC中，∠C=90°，它的内切圆O分别与AB、BC、CA相切于D、E、F，且BD=6，AD=4，则是⊙O的半径是（ ）
| A．6 | B．4 | C．3 | D．2 |
如图，
∵⊙O是直角三角形ABC的内切圆，
∴CEOF是正方形，
∴AF=AD=4；BE=BD=6
设⊙O的半径为r，则CE=CF=r
∴（4+r）2+（6+r）2=（4+6）2
∴r=2．
∴内切圆的半径是2．
故选D．
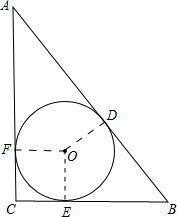
∵⊙O是直角三角形ABC的内切圆，
∴CEOF是正方形，
∴AF=AD=4；BE=BD=6
设⊙O的半径为r，则CE=CF=r
∴（4+r）2+（6+r）2=（4+6）2
∴r=2．
∴内切圆的半径是2．
故选D．
练习册系列答案
相关题目
