题目内容
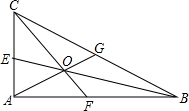
如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,若OD=2,求OC的长.
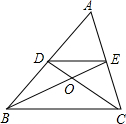

解法一:∵点D、E分别为AB、AC的中点,线段BE、CD相交于点O,
∴O点为△ABC的重心,
∴OC=2OD=4;
解法二:∵点D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=
BC,
∴∠ODE=∠OCB,∠OED=∠OBC,
∴△ODE∽△OCB,
∴OD:OC=DE:BC=1:2,
∴OC=2OD=4.
故OC的长为4.
∴O点为△ABC的重心,
∴OC=2OD=4;
解法二:∵点D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=
| 1 |
| 2 |
∴∠ODE=∠OCB,∠OED=∠OBC,
∴△ODE∽△OCB,
∴OD:OC=DE:BC=1:2,
∴OC=2OD=4.
故OC的长为4.

练习册系列答案
相关题目