题目内容
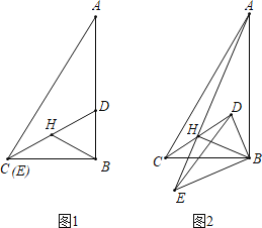
【题目】如图,Rt△ABC中,∠ACB=90°,AC=2,BC=4,CD是△ABC的中线,E是边BC上一动点,将△BED沿ED折叠,点B落在点F处,EF交线段CD于点G,当△DFG是直角三角形时,则CE=__________.

【答案】1或![]()
【解析】
根据题意分两种情形进行解答:①当∠DGF=90°时,作DH⊥BC于H.②当∠GDF=90°,作DH⊥BC于H,DK⊥FG于K.
解:①如图当∠DGF=90°时,作DH⊥BC于H.
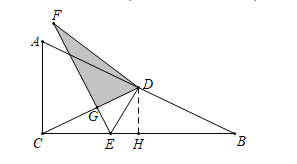
在Rt△ACB中,∠ACB=90°,AC=2,BC=4,
∵![]() ,
,
∵AD=DB
∴CD=![]() AB=
AB=![]() ,
,
∵DH∥AC,AD=DB,
∴CH=BH,
∴DH=DG=![]() AC=1,
AC=1,
∴CG=![]() -1,
-1,
∵DC=DB,
∴∠DCB=∠B,
∴cos∠DCB=cos∠B=![]() ,
,
∴CE=CG÷cos∠DCB=![]()
②如图当∠GDF=90°,作DH⊥BC于H,DK⊥FG于K.
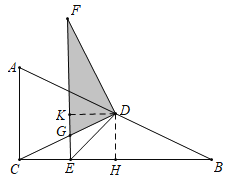
可得四边形DKEH是正方形,即EH=DH=1,
∵CH=BH=2,
∴.CE=1,
综上,满足条件的CE的值为1或![]() .
.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
x | … | 0 |
| 4 | … |
y | … | 0.37 | -1 | 0.37 | … |
则方程ax2+bx+1.37=0的根是( )
A.0或4B.![]() 或
或![]() C.1或5D.无实根
C.1或5D.无实根