题目内容
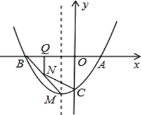
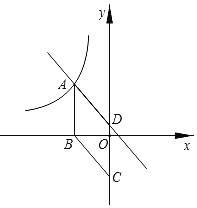
【题目】在平面直角坐标系中，我们把横、纵坐标均为整数的点叫做整点，已知反比例函数y＝
（m＜0）与y＝x2﹣5在第四象限内围成的封闭图形（包括边界）内的整点的个数为4，则实数m的取值范围为_____．
【答案】﹣5≤m＜﹣1
【解析】
根据题意可知抛物线在第四象限内的部分，然后根据反比例函数y＝
(m＜0)与y＝x2﹣5在第四象限内围成的封闭图形(包括边界)内的整点的个数为4，可以得到不等式组，从而可以求得m的取值范围．
∵y＝x2﹣5，
∴当x＝0时，y＝﹣5，当y＝0时，x＝±
，当x＝1时，y＝﹣4，
∴抛物线y＝x2﹣5在第四象限内的部分是(0，﹣5)到(，0)这一段曲线部分，
∵反比例函数y＝(m＜0)与y＝x2﹣5在第四象限内围成的封闭图形(包括边界)内的整点的个数为4，
∴
，
解得，﹣5≤m＜﹣1，
故答案为﹣5≤m＜﹣1
阳光试卷单元测试卷系列答案【题目】为了增强学生的疫情防控意识，响应“停课不停学”号召，某校组织了一次“疫情防控知识”专题网上学习，并进行了一次全校2500名学生都参加的网上测试．阅卷后，教务处随机抽取了100份答卷进行分析统计，发现考试成绩（
分）的最低分为51分，最高分为满分100分，并绘制了如下不完整的统计图表．请根据图表提供的信息，解答下列问题：
分数段（分） | 频数（人） | 频率 |
|
| 0.1 |
| 18 | 0.18 |
|
|
|
| 35 | 0.35 |
| 12 | 0.12 |
合计 | 100 | 1 |
（1）填空：
________，
________，
________；
（2）将频数分布直方图补充完整；
（3）该校对成绩为
的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为
，请你估算全校获得二等奖的学生人数；
（4）结合调查的情况，为了提高疫情防控意识，请你给学校提一条合理性建议．
【题目】数学学习小组根据函数学习的经验，对一个新函数
的图象和性质进行了如下探究：
列表，下表是函数
与自变量
的几组对应值
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
请直接写出
如图，在平面直角系
中，描出上表中各对对应值为坐标的点 （其中为横坐标，为纵坐标），并根据描出的点画出函数的图象
观察所画出的函数图象，写出该函数的性质（写一条性质即可）
请结合画出的函数图象与表格中数据，直接写出关于的不等式的解集：
