题目内容
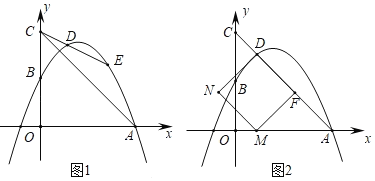
【题目】如图1,二次函数y![]() x2+bx+c的图象过A(5,0)和B(0,
x2+bx+c的图象过A(5,0)和B(0,![]() )两点,射线CE绕点C(0,5)旋转,交抛物线于D,E两点,连接AC.
)两点,射线CE绕点C(0,5)旋转,交抛物线于D,E两点,连接AC.
(1)求二次函数y![]() x2+bx+c的表达式;
x2+bx+c的表达式;
(2)连接OE,AE,当△CEO是以CO为底的等腰三角形时,求点E的坐标和△ACE的面积;
(3)如图2,射线CE旋转时,取DE的中点F,以DF为边作正方形DFMN.当点E和点A重合时,正方形DFMN的顶点M恰好落在x轴上.
①求点M的坐标;
②当点E和点A重合时,将正方形DFMN沿射线CE方向以每秒![]() 个单位长度平移.设运动时间为t秒.直接写出正方形DFMN落在x轴下方的面积S与时间t(0≤t≤4)的函数表达式.
个单位长度平移.设运动时间为t秒.直接写出正方形DFMN落在x轴下方的面积S与时间t(0≤t≤4)的函数表达式.
【答案】(1)y![]() x2+2x
x2+2x![]() ;(2)点E(4,
;(2)点E(4,![]() );△ACE的面积是
);△ACE的面积是![]() ;(3)①点M的坐标为(1,0);②S
;(3)①点M的坐标为(1,0);②S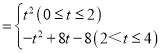 .
.
【解析】
(1)把A(5,0)和B(0,![]() )两点代入解析式,利用待定系数法求解即可,
)两点代入解析式,利用待定系数法求解即可,
(2)△CEO是以CO为底的等腰三角形时,可得点E、B关于抛物线对称轴对称.从而可得![]() 的坐标,再利用
的坐标,再利用![]() 可得答案,
可得答案,
(3) ①求解直线AC的表达式为:y=﹣x+5,利用对角线DM与AC的夹角为45°,得到![]() 从而利用D的坐标,得到M的坐标,②设正方形MFDN平移后为M'F'D'N',分
从而利用D的坐标,得到M的坐标,②设正方形MFDN平移后为M'F'D'N',分![]() 两种情况讨论即可得到答案.
两种情况讨论即可得到答案.
解:(1)将点A、B的坐标代入抛物线表达式得:
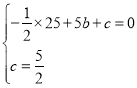 ,
,
解得![]() ,
,
故抛物线的表达式为:y![]() x2+2x
x2+2x![]() ①;
①;
(2)当C(0,5),△CEO是以CO为底的等腰三角形时,
则OC的中点(0,![]() )的纵坐标和点E的纵坐标相同,
)的纵坐标和点E的纵坐标相同,
而点B(0,![]() ),即点E、B关于抛物线对称轴对称.
),即点E、B关于抛物线对称轴对称.
∵抛物线的对称轴为直线x=2,
故点E的坐标为(4,![]() );
);
![]()
![]() OC|xE|
OC|xE|![]() OA|yE|
OA|yE|![]()
![]() 5×4
5×4![]() 5
5![]()

(3)①∵OA=OC=5,∴∠CAO=45°.
![]() 正方形DFMN,
正方形DFMN,
![]() 对角线DM与AC的夹角为45°,
对角线DM与AC的夹角为45°,
∴∠DMA=90°,即DM⊥x轴,
即点D、M的横坐标相同,
由A、C的坐标得:直线AC的表达式为:y=﹣x+5②,
联立①,②并解得:x=1或5(舍去5),
故x=1,故点D(1,4),
∴点M的坐标为(1,0);
②设正方形MFDN平移后为M'F'D'N',如图1,2所示;

由A、D的坐标得:DA![]() 4
4![]() ,
,
∵点F是AD的中点,故DA=2![]() ,即正方形MFDN的边长为2
,即正方形MFDN的边长为2![]() ,
,
∴正方形MFDN的面积为S1=(2![]() )2=8;
)2=8;
(Ⅰ)当0≤t≤2时,如图1所示,设M'F'交x轴于点H.
∵t秒时,正方形平移的距离为![]() t,
t,
∴MM'![]() t=M'H,
t=M'H,
∴S=S△M'MH![]() MM'M'H
MM'M'H![]() (
(![]() t)2=t2;
t)2=t2;
∵t秒时,正方形平移的距离为![]() t,则DD'
t,则DD'![]() t,
t,
∴AD'=AD﹣DD'=4![]() t=HD',
t=HD',
∴S=S1﹣S△AD'H=8![]() AD'×HD'=8
AD'×HD'=8![]()
![]() =﹣t2+8t﹣8,
=﹣t2+8t﹣8,
综上,S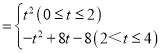 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案