Question

【题目】在平面直角坐标系xOy中，直线y＝kx（k≠0）与双曲线y＝（x＞0）交于点A（2，n）．

（1）求n及k的值；

（2）点B是y轴正半轴上的一点，且△OAB是等腰三角形，请直接写出所有符合条件的点B的坐标．

Answer 1

【答案】（1）n=4，k=2；（2）点B的坐标为（0，8），（0，2），（0，）．

【解析】

（1）由点A的横坐标利用反比例函数图象上点的坐标特征可求出n值，进而可得出点A的坐标，由点A的坐标利用待定系数法可求出k值；

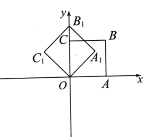
（2）分AB＝AO，OA＝OB，BO＝BA三种情况考虑：①当AB＝AO时，利用等腰三角形的性质可求出CB1的长度，结合点C的坐标可得出点B1的坐标；②当OA＝OB时，由点A的坐标利用勾股定理可求出OA的长度，利用等腰三角形的性质可得出OB2的长度，进而可得出点B2的坐标；③当BO＝BA时，设OB3＝m，则CB3＝4﹣m，AB3＝m，在Rt△ACB3中利用勾股定理可得出关于m的方程，解之即可得出点B3的坐标．综上，此题得解．

（1）∵点A（2，n）在双曲线y＝上，

∴n＝＝4，

∴点A的坐标为（2，4）．

将A（2，4）代入y＝kx，得：4＝2k，

解得：k＝2．

（2）分三种情况考虑，过点A作AC⊥y轴于点C，如图所示．

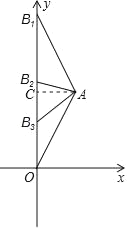
①当AB＝AO时，CO＝CB1＝4，

∴点B1的坐标为（0，8）；

②当OA＝OB时，∵点A的坐标为（2，4），

∴OC＝4，AC＝2，

∴OA＝，

∴OB2＝2，

∴点B2的坐标为（0，2）；

③当BO＝BA时，设OB3＝m，则CB3＝4﹣m，AB3＝m，

在Rt△ACB3中，AB32＝CB32+AC2，即m2＝（4﹣m）2+22，

解得：m＝，

∴点B3的坐标为（0，）．

综上所述：点B的坐标为（0，8），（0，2），（0，）．