Question

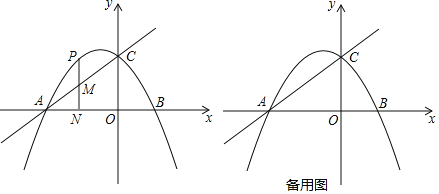
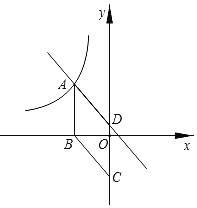
【题目】如图，在直角坐标系中，菱形ABCD的边长为5，面积为15，点A在双曲线y＝上，点B在x轴上，C、D在y轴上．

（1）求顶点A的坐标和k的值．

（2）求直线AD的解析式．

Answer 1

【答案】（1）点A的坐标为（﹣3，5），k＝﹣15；（2）y＝﹣x＋1．

【解析】

（1）连接BD，作DE⊥AB，由S菱形ABCD＝2S△ABD，即可求出DE，即可得出点A的横坐标；把点A的坐标，代入y＝，即可求出k值；

（2）设点D的坐标为（0，y），由AD＝5，根据两点间的距离公式，可求出y值；再设直线AD的解析式为y＝k1x＋b，把点A、D的坐标代入，可求出k1的值，即可解答；

解：（1）如图，连接BD，作DE⊥AB，

∴S菱形ABCD＝2S△ABD，S△ABD＝AB×ED，

∵菱形ABCD的面积为15，AB＝5，

∴2××5×ED＝15，

解得，DE＝3，

∴点A的坐标为：（﹣3，5）；

又∵点A在双曲线y＝上，

∴5＝，

∴k＝﹣15；

（2）设点D的坐标为（0，y），

∵四边形ABCD为菱形，

∴AB＝AD＝5，

∴，

解得y＝9（舍去），y＝1，

∴点D的坐标为（0，1）．

设直线AD的解析式为y＝k1x＋b，

∵直线AD过A、D两点，

∴，

解得.

∴直线AD的解析式为：y＝﹣x＋1．