题目内容
17.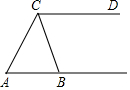 如图,在△ABC中,已知∠CAB=60°,AB∥CD.
如图,在△ABC中,已知∠CAB=60°,AB∥CD.(1)请用尺规作图,在图中直接作出∠CAB的平分线交CB于点E,交CD于点F;(不写作法,保留作图痕迹)
(2)在(1)的条件下,求出∠AFC的度数;
(3)在(1)的条件下,若AF⊥CB,试确定AB和CF的数量关系,并证明你的结论.
分析 (1)根据角平分线的尺规作图方法,进行画图即可得到AF;
(2)根据角平分线的定义以及平行线的性质,得出∠AFC=∠BAF=30°;
(3)根据等角对等边,得出AB=AC,CF=AC,即可得到AB=CF.
解答 解:(1)如图所示,AF即为所求;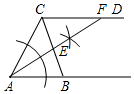
(2)∵∠CAB=60°,AF平分∠CAB,
∴∠BAF=30°,
∵AB∥CD,
∴∠AFC=∠BAF=30°;
(3)AB=CF.
理由:∵AF⊥CB,
∴∠AEB=∠AEC=90°,
∵AE平分∠BAC,
∴∠ABE=∠ACE,
∴AB=AC,
∵∠CAE=∠BAE=∠AFC,
∴CF=AC,
∴AB=CF.
点评 本题主要考查了角平分线的作图以及三角形内角和定理的运用,复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 直角三角形 | B. | 线段 | C. | 角 | D. | 等腰梯形 |
2.扇形周长为1,当扇形的半径为R时,扇形有最大面积S,则R和S的值为( )
| A. | $\frac{1}{4}$,$\frac{1}{16}$ | B. | $\frac{1}{2}$,$\frac{1}{8}$ | C. | $\frac{1}{4}$,$\frac{1}{8}$ | D. | $\frac{1}{2}$,$\frac{1}{16}$ |
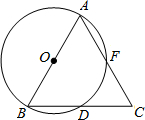 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.