Question

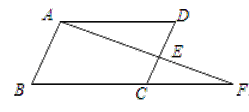
【题目】如图，在△ABC中，∠C＝90°，将△ACE沿着AE折叠以后C点正好落在AB边上的点D处．

（1）当∠B＝28°时，求∠AEC的度数；

（2）当AC＝6，AB＝10时，

①求线段BC的长；

②求线段DE的长．

Answer 1

【答案】(1) 59°;(2) ①8, ②3

【解析】

（1）在Rt△ABC中，利用互余得到∠BAC=62°，再根据折叠的性质得∠CAE=∠CAB=31°，然后根据互余可计算出∠AEC=59°；

（2）①在Rt△ABC中，利用勾股定理即可得到BC的长；②设DE=x，则EB=BC-CE=8-x，依据勾股定理可得，Rt△BDE中DE2+BD2=BE2，再解方程即可得到DE的长．

（1）在Rt△ABC中，∠ABC＝90°，∠B＝28°，

∴∠BAC＝90°﹣28°＝62°，

∵△ACE沿着AE折叠以后C点正好落在点D处，

∴∠CAE＝∠CAB＝×62°＝31°，

Rt△ACE中，∠ACE＝90°

∴∠AEC＝90°﹣31°＝59°．

（2）①在Rt△ABC中，AC＝6，AB＝10，

∴BC＝．

②∵△ACE沿着AE折叠以后C点正好落在点D处，

∴AD＝AC＝6，CE＝DE，

∴BD＝AB﹣AD＝4，

设DE＝x，则EB＝BC﹣CE＝8﹣x，

∵Rt△BDE中，DE2+BD2＝BE2，

∴x2+42＝（8﹣x）2，

解得x＝3．

即DE的长为3．