题目内容
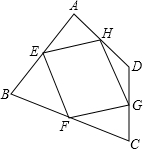 如图,在四边形ABCD中,点E、F、G、H分别是各边的中点,则按要求完成下列题目.
如图,在四边形ABCD中,点E、F、G、H分别是各边的中点,则按要求完成下列题目.(1)四边形EFGH是
平行四边
平行四边
形;(2)四边形ABCD应满足什么条件时,四边形EFGH是菱形,并证明你的结论.
分析:(1)连接BD,再利用三角形中位线定理可得FG∥BD,FG=
BD,EH∥BD,EH=
BD.进而得到FG∥EH,且FG=EH,可根据一组对边平行且相等的四边形是平行四边形证出结论;
(2)菱形是邻边相等的平行四边形.由(1)知,四边形EFGH是平行四边形,所以只需四边形ABCD的对角线相等即可证得平行四边形EFGH是菱形.
| 1 |
| 2 |
| 1 |
| 2 |
(2)菱形是邻边相等的平行四边形.由(1)知,四边形EFGH是平行四边形,所以只需四边形ABCD的对角线相等即可证得平行四边形EFGH是菱形.
解答: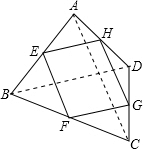 (1)解:如图,连接BD.
(1)解:如图,连接BD.
∵F,G分别是BC,CD的中点,
所以FG∥BD,FG=
BD.
∵E,H分别是AB,DA的中点.
∴EH∥BD,EH=
BD.
∴FG∥EH,且FG=EH.
∴四边形EFGH是平行四边形;
故填:平行四边;
(2)AC=BD.
理由如下:如图,连AC.
由(1)知,四边形EFGH是平行四边形,且FG=
BD,HG=
AC,
∴当AC=BD时,FG=HG,
∴平行四边形EFGH是菱形.
 (1)解:如图,连接BD.
(1)解:如图,连接BD.∵F,G分别是BC,CD的中点,
所以FG∥BD,FG=
| 1 |
| 2 |
∵E,H分别是AB,DA的中点.
∴EH∥BD,EH=
| 1 |
| 2 |
∴FG∥EH,且FG=EH.
∴四边形EFGH是平行四边形;
故填:平行四边;
(2)AC=BD.
理由如下:如图,连AC.
由(1)知,四边形EFGH是平行四边形,且FG=
| 1 |
| 2 |
| 1 |
| 2 |
∴当AC=BD时,FG=HG,
∴平行四边形EFGH是菱形.
点评:此题主要考查了中点四边形,关键是掌握三角形中位线定理,三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
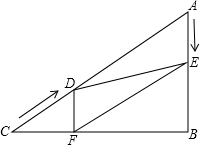 (2013•赤峰)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(2013•赤峰)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.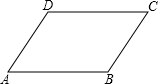 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.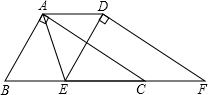 如图,在Rt△ABC中,∠BAC=90°,将△ABC沿线段BC向右平移得到△DEF,使CE=AE,连结AD、AE、CD,则下列结论:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四边形AECD为菱形,其中正确的共有( )
如图,在Rt△ABC中,∠BAC=90°,将△ABC沿线段BC向右平移得到△DEF,使CE=AE,连结AD、AE、CD,则下列结论:①AD∥BE且AD=BE;②∠ABC=∠DEF;③ED⊥AC;④四边形AECD为菱形,其中正确的共有( )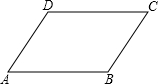 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.