题目内容
【题目】已知矩形ABCD中,AB=10,BC=4,点P从点A出发,以每秒1个单位长度沿AB方向向B运动,点Q从点C出发,以每秒2个单位长度沿CD方向向D运动,如果P、Q两点同时出发,问几秒后以△BPQ是直角三角形?
【答案】P、Q两点同时出发,问![]() s或2s或
s或2s或![]() 秒后以△BPQ是直角三角形.
秒后以△BPQ是直角三角形.
【解析】
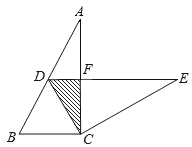
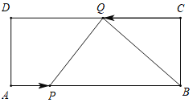
由矩形的性质可得AB=CD=10,BC=AD=4,∠A=∠C=90°,AB∥CD,进而确定∠CQB=∠PBQ,①如图1,当∠ PQB=90°时,过P作PE⊥CD于E,根据相似三角形的性质可得t=2或t=![]() ;②如图2,当∠BPQ=90°时,根据矩形的性质即可得到结论.
;②如图2,当∠BPQ=90°时,根据矩形的性质即可得到结论.
解:∵四边形ABCD是矩形,
∴AB=CD=10,BC=AD=4,∠A=∠C=90°,AB∥CD,
∴∠CQB=∠PBQ,
∵△BPQ是直角三角形,
∴①如图1,∠PQB=90°时,
过P作PE⊥CD于E,
则DE=AP,PE=AD=4,
∵∠PEQ=∠BQP=∠C=90°,
∴∠EPQ+∠PQE=∠PQE+∠CQB=90°,
∴∠EPQ=∠CQB,
∴△PQE∽△QBC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:t=2,t=![]() ,
,
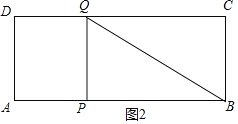
②如图1,当∠BPQ=90°时,
∴∠APQ=90°,
∴四边形APQD和四边形PBCQ是矩形,
∴CQ=PB,
∴10﹣t=2t,
解得:t=![]() ,
,
综上所述,P、Q两点同时出发,问![]() s或2s或
s或2s或![]() 秒后以△BPQ是直角三角形.
秒后以△BPQ是直角三角形.


练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目