题目内容
【题目】在平面直角坐标系中，对于点P（x，y）和Q（x，y′），给出如下定义：如果y′＝
，那么称点Q为点P的“伴随点”．
例如：点（5，6）的“伴随点”为点（5，6）；点（﹣5，6）的“伴随点”为点（﹣5，﹣6）．
（1）直接写出点A（2，1）的“伴随点”A′的坐标．
（2）点B（m，m+1）在函数y＝kx+3的图象上，若其“伴随点”B′的纵坐标为2，求函数y＝kx+3的解析式．
（3）点C、D在函数y＝﹣x2+4的图象上，且点C、D关于y轴对称，点D的“伴随点”为D′．若点C在第一象限，且CD＝DD′，求此时“伴随点”D′的横坐标．
（4）点E在函数y＝﹣x2+n（﹣1≤x≤2）的图象上，若其“伴随点”E′的纵坐标y′的最大值为m（1≤m≤3），直接写出实数n的取值范围．
【答案】（1）A'的坐标为（2，1）；（2）①当m≥0时，y＝﹣x+3；②m＜0时，y＝
x+3；（3）D′的横坐标为
；（4）﹣2≤n≤0、1≤n≤3.
【解析】
（1）由题意即可求解；
（2）分m≥0、m＜0两种情况分别求解即可；
（3）设点C的横坐标为n，点C在函数y＝﹣x2+4的图象上，CD＝DD′，即可求解；
（4）通过画图即可求解．
解：（1）由题意得：点A'的坐标为（2，1）
（2）①当m≥0时，
m+1＝2，m＝1
∴B（1，2）
∵点B在一次函数y＝kx图象上，
∴k+3＝2，
解得：k＝+1
∴一次函数解析式为y＝﹣x+3
②m＜0时，
m+1＝﹣2，m＝﹣3
∴B（﹣3，﹣2）
∵点B在一次函数y＝kx+3图象上，
∴﹣3k+3＝﹣2
解得：k＝
一次函数解析式为y＝x+3．
（3）设点C的横坐标为n，点C在函数y＝﹣x2+4的图象上，
∴点C的坐标为（n，﹣n2+4），
∴点D的坐标为（﹣n，﹣n2+4），D′（﹣n，n2﹣4）
∵CD＝DD′，
∴2n＝2（n2+4），
解得：n＝
；
∵点C在第一象限，
∴D′的横坐标为
；
（4）﹣2≤n≤0、1≤n≤3，
当左边的抛物线在上方时，如图①、图②：﹣2≤n≤0；
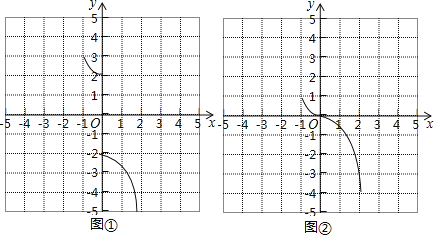
当右边的抛物线在上方时，如图③、图④：1≤n≤3．
【题目】“重整行装再出发，驰而不息再争创”，2018年5月8日兰州市召开了新一轮全国文明城市创建启动大会.某校为了更好地贯彻落实创建全国文明城市目标，举办了“我是创城小主人”的知识竞赛.该校七年级、八年级分别有300人，现从中各随机抽取10名同学的测试成绩进行调查分析，成绩如下：
七年级 | 85 | 65 | 84 | 78 | 100 | 78 | 85 | 85 | 98 | 83 |
八年级 | 96 | 60 | 87 | 78 | 87 | 87 | 89 | 100 | 83 | 96 |
整理、描述数据：
分数段 |
|
|
|
|
七年级人数 | 1 | 2 | 5 | 2 |
八年级人数 | 1 | 1 | 5 | 3 |
分析数据：
年级 | 平均数 | 中位数 | 众数 |
七 | 84.1 | _______ | 85 |
八 | 86.3 | 87 | ______ |
得出结论：
（1）根据上述数据，将表格补充完整；
（2）估计该校七、八两个年级学生在本次测试成绩中可以取得优秀的人数
共有多少人？
（3）你认为哪个年级知识掌握的总体水平较好，说明理由.
