题目内容
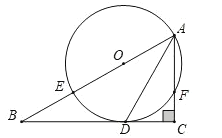
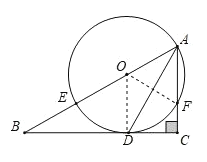
【题目】如图,E是![]() 的斜边AB上一点,以AE为直径的
的斜边AB上一点,以AE为直径的![]() 与边BC相切于点D,交边AC于点F,连结AD.
与边BC相切于点D,交边AC于点F,连结AD.
(1)求证:AD平分![]() .
.
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结OD,由切线的性质及∠C=90°可得OD∥AC,进而得∠CAD=∠ODA,再由OA=OD得∠OAD=∠ODA,等量代换即可得证;
(2)先由∠CAD=25°求得∠EOF=100°,再利用弧长公式计算即可.
(1)如图,连结OD.
∵⊙O与边BC相切于点D,
∴OD⊥BC,
∴∠ODB=90°.
∵∠C=90°,
∴∠C=∠ODB=90°,
∴OD∥AC,
∴∠CAD=∠ODA.
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠CAD.
∴AD平分∠BAC.
(2)如图,连结OF.
∵AD平分∠BAC,且∠CAD=25°,
∴![]() ,
,
∴∠EOF=100°,
∴![]() 的长为
的长为![]() .
.

练习册系列答案
相关题目