题目内容
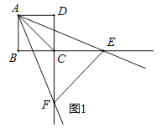
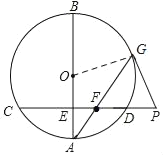
【题目】已知,AB为⊙O的直径,弦CD⊥AB于点E,在CD的延长线上取一点P,PG与⊙O相切于点G,连接AG交CD于点F.
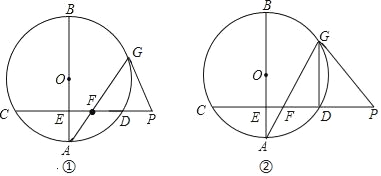
(Ⅰ)如图①,若∠A=20°,求∠GFP和∠AGP的大小;
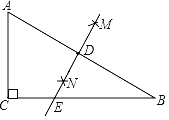
(Ⅱ)如图②,若E为半径OA的中点,DG∥AB,且OA=2![]() ,求PF的长.
,求PF的长.
【答案】(Ⅰ)∠GFP=70°,∠AGP=70°;(Ⅱ)PF=4.
【解析】
(Ⅰ)连接OG,在Rt△AEF中,∠A=20°,可得∠GFP=∠EFA=70°,因为OA=OG,所以∠OGA=∠A=20°,因为PG与⊙O相切于点G,得∠OGP=90°,可得∠AGP=90°﹣20°=70°.;
(Ⅱ)如图,连结BG,OG,OD,AD,证明△OAD为等边三角形,得∠AOD=60°,所以∠AGD=30°,因为DG∥AB,所以∠BAG=∠AGD=30°,在Rt△AGB中可求得AG=6,在Rt△AEF中可求得AF=2,再证明△GFP为等边三角形,所以PF=FG=AG﹣AF=6﹣2=4.
解:(Ⅰ)连接OG,
∵CD⊥AB于E,
∴∠AEF=90°,
∵∠A=20°,
∴∠EFA=90°﹣∠A=90°﹣20°=70°,
∴∠GFP=∠EFA=70°,
∵OA=OG,
∴∠OGA=∠A=20°,
∵PG与⊙O相切于点G,
∴∠OGP=90°,
∴∠AGP=∠OGP﹣∠OGA=90°﹣20°=70°.
(Ⅱ)如图,连结BG,OG,OD,AD,
∵E为半径OA的中点,CD⊥AB,
∴OD=AD=OA,
∴△OAD为等边三角形,
∴∠AOD=60°,
∴∠AGD=![]() ∠AOD=30°,
∠AOD=30°,
∵DG∥AB,
∴∠BAG=∠AGD=30°,
∵AB为⊙O的直径,OA=2![]() ,
,
∴∠AGB=90°,AB=4![]() ,
,
∴AG=ABcos30°=6,.
∵OG=OA,
∴∠OGA=∠BAG=30°,
∵PG与⊙O相切于点G,∴∠OGP=90°,
∴∠FGP=90°﹣30°=60°,
∵∠AEF=90°,AE=![]() ,∠BAG=30°,
,∠BAG=30°,
∴AF=2,∠GFP=∠EFA=60,
∴△GFP为等边三角形,
∴PF=FG=AG﹣AF=6﹣2=4.

 名校课堂系列答案
名校课堂系列答案【题目】某数学兴趣小组的同学在研究函数![]() 的图象时,先对函数
的图象时,先对函数![]() 的图象进行了如下探索.
的图象进行了如下探索.
![]() ①列表:列出
①列表:列出![]() 与
与![]() 的几组对应值如下:
的几组对应值如下:
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
②描点:根据表中数据描点如图所示;
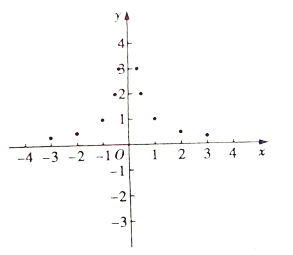
③连线:请在图中画出函数![]() 的图象;
的图象;
④观察图象,写出两条关于该函数的性质.
![]() 根据以上探究结果,完成下列问题:
根据以上探究结果,完成下列问题:
①函数![]() 中,自变量
中,自变量![]() 的取值范围为 ;
的取值范围为 ;
②函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
③写出两条关于函数![]() 的性质;
的性质;
④直接写出不等式![]() 的解集.
的解集.