题目内容
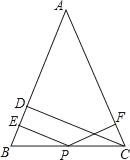
【题目】如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,连结AO,则图中共有全等三角形的对数为( )

A. 2对 B. 3对 C. 4对 D. 5对
【答案】C
【解析】
先根据条件,利用AAS可知△ADB≌△AEC,然后再利用HL、ASA即可判断△AOE≌△AOD,△BOE≌△COD,△AOC≌△AOB.
∵AB=AC,BD⊥AC于D,CE⊥AB于E,
∴∠ADB=∠AEC=90°,
∵∠A为公共角,
∴△ADB≌△AEC,(AAS)
∴AE=AD,∠B=∠C
∴BE=CD,
∵AE=AD,OA=OA,∠ADB=∠AEC=90°,
∴△AOE≌△AOD(HL),
∴∠OAC=∠OAB,
∵∠B=∠C,AB=AC,∠OAC=∠OAB,
∴△AOC≌△AOB.(ASA)
∵∠B=∠C,BE=CD,∠ODC=∠OEB=90°,
∴△BOE≌△COD(ASA).
综上:共有4对全等三角形,
故选C.

练习册系列答案
相关题目
【题目】下表中所列x,y的数值是某二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7 , 根据表中所提供的信息,以下判断正确的是( ).
①a>0;
②9<m<16;
③k≤9;
④b2≤4a(c﹣k).
x | … | x1 | x2 | x3 | x4 | x5 | x6 | x7 | … |
y | … | 16 | m | 9 | k | 9 | m | 16 | … |
A.①②
B.③④
C.①②④
D.①③④