题目内容
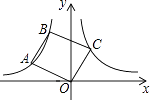
【题目】在平面直角坐标系中,点A的坐标是(0,6),点B的坐标是(6,0).
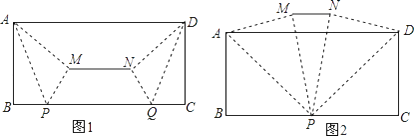
(1)如图1,点C的坐标是(﹣2,0),BD⊥AC于D交y轴于点E.求点E的坐标;
(2)在(1)的条件下求证:OD平分∠CDB;
(3)如图2,点F为AB中点,点G为x正半轴点B右侧一动点,过点F作FG的垂线FH,交y轴的负半轴于点H,那么当点G的位置不断变化时,S△AFH﹣S△FBG的值是否发生变化?若变化,请说明理由;若不变化,请求出相应结果.

【答案】(1)点E的坐标为(0,2);(2)详见解析;(3)S△AFH﹣S△FEG=9不发生变化,理由详见解析.
【解析】
(1)易得OA=OB,由∠ACO+∠CAO=90°,∠BCD+∠CBE=90°,可得∠CAO=∠CBE,可证得△AOC≌△BOE,可得OE=OC,可得E点左边;
(2)过点O作OM⊥BD于M,ON⊥AC于N,由△AOC≌△BOE,可得S△AOC=S△BOE,由AC=BE,可得OM=ON,所以点O一定在∠CDB的角平分线上,即OD平分∠CDB;
(3))S△AFH﹣S△FEG=9不发生变化,理由如下:连接OF,可证得△FOH≌△FBG,可得
S△AOC=S△BOE,可得S△AFH﹣S△FBG=S△AFH﹣S△FOH=S△FOA=![]() =9.
=9.
解:(1)∵x轴⊥y轴
∴∠AOC=∠BOE=90°
∴∠ACO+∠CAO=90°
∵BD⊥AC
∴∠BCD+∠CBE=90°
∴∠CAO=∠CBE,
∵点A,B的坐标分别为(0,6),(6,0)
∴OA=OB=6,
在△AOC和△BOE中
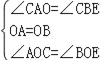
∴△AOC≌△BOE(ASA)
∴OE=OC,
∵点C的坐标为(﹣2,0)
∴OC=OE=2
∴点E的坐标为(0,2)
(2)过点O作OM⊥BD于M,ON⊥AC于N

∵△AOC≌△BOE
∴S△AOC=S△BOE,AC=BE,
∴![]() ACON=
ACON=![]() BCOM
BCOM
∴OM=ON,
∴点O一定在∠CDB的角平分线上
即OD平分∠CDB;
(3)S△AFH﹣S△FEG=9不发生变化,理由如下:
连接OF
∵△AOB是等腰直角三角形且点F为AB的中点
∴OF⊥AB,OF=FB,OF平分∠AOB
∴∠OFB=∠OFH+∠HFB=90°
又∵FG⊥FH
∴∠HFG=∠BFG+∠HFB=90°
∴∠OFH=∠BFG
∵∠FOB=![]()
∴∠FOH=∠FOB+∠HOB=45°+90°=135°
又∵∠FBG=180°﹣∠ABO=180°﹣45°=135°
∴∠FOH=∠FBG
在△FOH和△FBG中
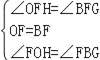
∴△FOH≌△FBG(ASA)
∴S△AOC=S△BOE
∴S△AFH﹣S△FBG
=S△AFH﹣S△FOH
=S△FOA=![]() .
.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案