题目内容
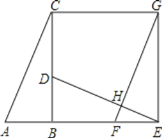
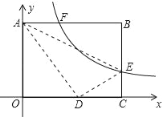
【题目】如图,将矩形ABCO放在平面直角坐标系中,其中顶点B的坐标为(5,3),E是BC边上一点,将△ABE沿AE翻折,点B刚好与OC边上的点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F,则线段AF的长为_____.
的图象与边AB交于点F,则线段AF的长为_____.
【答案】![]()
【解析】
根据△ABE与△ADE是全等可得BE=DE,设BE=a=DE, CE=3-a,在Rt△AOD中,AD=AB=5,AO=3,由勾股定理![]() ,可得a的值,可求出反比例函数的表达式,可求出AF的长.
,可得a的值,可求出反比例函数的表达式,可求出AF的长.
解:根据题目条件可知, △ABE与△ADE是全等的,所以BE=DE,
设BE=a=DE, CE=3-a,
在Rt△AOD中,AD=AB=5,AO=3,由勾股定理![]() ,
,
即OD=![]() =4,
=4,
所以DC=OC-OD=1,
在Rt△DCE中, 由勾股定理![]() ,
,
即![]() ,求出a=
,求出a=![]() ,CE=
,CE=![]() ,
,
所以E(5,![]() ),
),
因为点E在反比例反函数上, 可得k =5![]()
![]() =
=![]() ,即可y=
,即可y=![]() ,
,
又因为点F在反比例函数上, 设F(b,3),
可得:b=![]() =
=![]() ,即AF的长为
,即AF的长为![]() .
.
故答案:![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目