题目内容
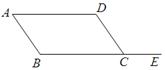
如图,在□ABCD中,E为BC边上一点,且AB=AE.
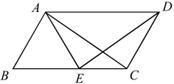
(1)求证:△ABC ≌△EAD;
(2)若AE平分∠DAB,∠EAC=25º,求∠AED的度数.

(1)求证:△ABC ≌△EAD;
(2)若AE平分∠DAB,∠EAC=25º,求∠AED的度数.
见解析
试题分析:
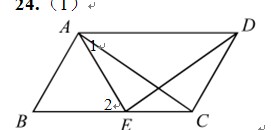
∵在□ABCD中,AD∥BC,BC=AD…………(1分)
∴∠1=∠2………………………………………(2分)
又∵AB=AE,∴∠B=∠2,∴∠B=∠1……(3分)
∴△ABC ≌△EAD(SAS)……………………(4分)
(2)先证△ABE为等边三角形,得∠BAE=60º…………………………………(5分)
∴∠AED=∠BAC=∠BAE+∠EAC=60º+25º=85º………………………(7分)
点评: 本题属于难度较大的试题,考生遇到此类试题时要注意:⑴三边相等的三角形是等边三角形(定义)
⑵三个内角都相等(为60度)的三角形是等边三角形
⑶有一个角是60度的等腰三角形是等边三角形
(4) 两个内角为60度的三角形是等边三角形
说明:可首先判断三角形是等腰三角形。
等边三角形的性质与判定理解:
首先,明确等边三角形定义。三边相等的三角形叫做等边三角形,也称正三角形。
其次,明确等边三角形与等腰三角形的关系。等边三角形是特殊的等腰三角形,等腰三角形不一定是等边三角形。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 BD,E、F、G、H分别为AB、BC、CD、DA的中点.
BD,E、F、G、H分别为AB、BC、CD、DA的中点.
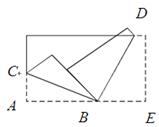
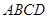 中,
中,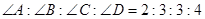 ,则
,则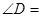 ;
; 、6
、6