题目内容
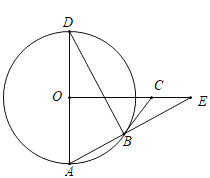
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 的弦,
的弦,![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 在
在![]() 上, 满足
上, 满足![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() , 求线段
, 求线段![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OB,如图,根据圆周角定理得到∠ABD=90°,再根据等腰三角形的性质和已知条件证出∠OBC=90°,即可得出结论;
(2)根据圆周角定理得到∠ABD=90°,得到∠A=60°,求得∠E=30°,根据等腰三角形的性质得到CE=CB,根据三角形外角的性质得到∠BCO=60°,解直角三角形即可得到结论.
(1)证明:连接OB,如图,
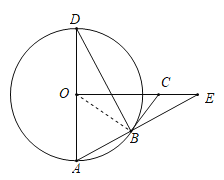
∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠A+∠ADB=90°,
∵OA=OB,
∴∠A=∠OBA,
∵∠CBE=∠ADB,
∴∠OBA+∠CBE=90°,
∴∠OBC=180°-90°=90°,
∴BC⊥OB,
∴BC是⊙O的切线;
(2)∵AD是⊙O的直径,
∴∠ABD=90°,
∴∠A=60°,
∵OE⊥AD,
∴∠AOE=90°,
∴∠E=30°,
∵∠CBE=30°,
∴∠CBE=∠E=30°,
∴CE=CB,
∴∠BCO=60°,
在![]() 中
中
![]()
![]()
∴BC=![]() OB=
OB=![]() ,
,
∴CE=![]() .
.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目