题目内容
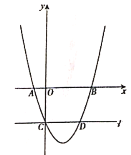
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 分别落在点
分别落在点![]() ,
,![]() ,
,![]() 处.
处.
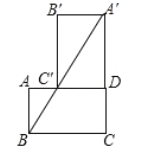
(1)直接填空:当![]() 时,点
时,点![]() 所经过的路径的长为___________;
所经过的路径的长为___________;
(2)若点![]() ,
,![]() ,
,![]() 在同一直线上,求
在同一直线上,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由题意可知点B经过的路径是以点D为圆心,以BD的长为半径,圆心角为90°的弧长,然后用勾股定理求得BD的长,再利用弧长公式求解即可;
(2)由AB=m,根据平行线的性质列出比例式求出m的值,根据正切的定义求出tan∠BA′C,根据∠ABA′=∠BA′C解答即可.
解:(1)由题意可知,点B经过的路径是以点D为圆心,以BD的长为半径,圆心角为90°的弧长,
∴连接![]() ,
,
当m=1时,AB=1,在矩形ABCD中,AD=BC=2
∴在Rt△ABD中,![]()
∴此时点![]() 所经过的路径的长为
所经过的路径的长为![]()
故答案为:![]() .
.
(2)由题意AB=m,则CD=m,A′C=m+2,
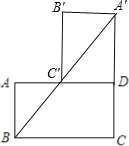
∵AD∥BC,
∴![]() ,即
,即![]() ,
,
解得,![]() ,
,![]() (舍去),
(舍去),
∵AB∥CD,
∴∠ABA′=∠BA′C,
tan∠BA′C=![]() ,
,
∴tan∠ABA′=![]() ,
,

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目