题目内容
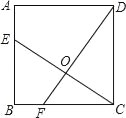
【题目】如图,已知四边形ABCD内接于⊙O,A是弧BDC的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且弧BF=弧AD.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.

【答案】(1)见解析;(2)![]()
【解析】分析:(1)利用圆的内接四边形角的性质,可得到角相等,再利用题目中给定的弧相等,所以圆周角相等,所以可证明三角形相似.(2)初中阶段求三角函数值,必须构造一个直角三角形或把要求的角转移到一个直角三角形中,本题由(1)的结论把∠CAD=∠AEC,在直角三角形AEC中,求三角函数.
详解:
(1)证明:∵四边形ABCD内接于⊙O,
∴∠CDA+∠ABC=180°.又∵∠ABE+∠ABC=180°,
∴∠CDA=∠ABE.
∵弧BF=弧AD∴∠DCA=∠BAE,∴△ADC∽△EBA.
(2)解:∵A是弧BDC的中点,∴弧AB=弧AC,∴AB=AC=8.
由(1)可知△ADC∽△EBA,∴∠CAD=∠AEC,![]() ,
,
∴tan∠CAD=tan∠AEC=![]() .
.

练习册系列答案
相关题目