题目内容
【题目】在平面直角坐标系中,直线l1:![]() 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2:![]() (
(![]() ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.
(1)求点A,B的坐标;
(2)如图,当![]() =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与![]() 轴围成的△BDE的面积;
轴围成的△BDE的面积;
(3)若直线l1,l2与![]() 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2:![]() (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.
①求![]() 的值;
的值;
②若![]() ,,求
,,求![]() 的取值范围.
的取值范围.

【答案】(1)A(0,6)B(3,0)(2)8(3)①![]() ;②
;②![]()
【解析】
(1)根据![]() ,令x=0,得到y=6;令y=0,得到x=3,即可解答;
,令x=0,得到y=6;令y=0,得到x=3,即可解答;
(2)当![]() =2时,求出直线l2:
=2时,求出直线l2:![]() 与x轴交点D的坐标,从而求出DB的长,再把
与x轴交点D的坐标,从而求出DB的长,再把
两直线的解析式组成方程组求出点E的坐标,根据三角形的面积公式求出△BDE的面积;
(3)①若直线l1,l2与![]() 轴不能围成三角形,则直线l2与l1平行或直线l2经过点B,从而求出k的值;②根据k的值分别求出直线l2解析式,再根据点P (a,b)在直线l2 上得到a与b的关系式,从而确定
轴不能围成三角形,则直线l2与l1平行或直线l2经过点B,从而求出k的值;②根据k的值分别求出直线l2解析式,再根据点P (a,b)在直线l2 上得到a与b的关系式,从而确定![]() 的取值范围.
的取值范围.
(1)∵![]() ,
,
∴令x=0,得到y=6;令y=0,得到x=3,
则A(0,6),B(3,0);
(2)当![]() =2时,直线l2:
=2时,直线l2:![]()
令y=0,得到x=-1,
∴D(-1,0)
∴BD=4
由![]()
解得:![]()
∴点E坐标为(1,4)
∴![]() 4=8
4=8
(3)①若直线l1,l2与![]() 轴不能围成三角形,则直线l2与l1平行或直线l2经过点B,
轴不能围成三角形,则直线l2与l1平行或直线l2经过点B,
当直线l2与l1平行,k=-2,当直线l2经过点B时,![]() =0,则
=0,则![]() =-
=-![]()
∴k=-2或-![]()
②当k=-2时,直线l2的解析式为:![]() ,
,
∵点P(a,b)在直线l2上,∴b=-2a+2
∴![]() =a-2a+2=2-a
=a-2a+2=2-a
∵点P(a,b)在第一象限
∴![]()
解得:0![]()
∴1![]() 2-a
2-a![]() ,即1
,即1![]()
当k=-![]() 时,直线l2的解析式为:
时,直线l2的解析式为:![]() ,
,
∵点P(a,b)在直线l2上,∴b=![]() a+2
a+2
∴![]() =a-
=a-![]() a+2=
a+2=![]() a+2
a+2
∵点P(a,b)在第一象限
∴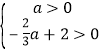
解得:0![]()
∴2![]() a+2
a+2![]() ,即2
,即2![]()
综上所述:![]() 的取值范围为:1
的取值范围为:1![]() 或2
或2![]()






