题目内容
【题目】如图,在Rt△ABO中,斜边AB=1,若OC∥BA,∠AOC=36°,则( )
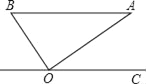
A. 点B到AO的距离为sin54°
B. 点A到OC的距离为sin36°sin54°
C. 点B到AO的距离为tan36°
D. 点A到OC的距离为cos36°sin54°
【答案】B
【解析】分析:过A作AD![]() OC,利用平行线性质可知∠A=∠AOC,所以可以解直角三角形,得到BO ,AO,再解直接三角形,可以得到A到OC的距离.
OC,利用平行线性质可知∠A=∠AOC,所以可以解直角三角形,得到BO ,AO,再解直接三角形,可以得到A到OC的距离.
详解:解:B到AO的距离是指BO的长,
∵AB∥OC,
∴∠BAO=∠AOC=36°,
∵在Rt△BOA中,∠BOA=90°,AB=1,
∴sin36°=![]() ,
,
∴BO=ABsin36°=sin36°,
故A、C选项错误;
过A作AD⊥OC于D,则AD的长是点A到OC的距离,
∵∠BAO=36°,∠AOB=90°,
∴∠ABO=54°,
∵sin36°=![]() ,
,
∴AD=AOsin36°,
∵sin54°=![]() ,
,
∴AO=ABsin54°,
∵AB=1,
∴AD=ABsin54°sin36°=1×sin54°sin36°=sin54°sin36°,
故B选项正确,D选项错误;
故选:B.

 阅读快车系列答案
阅读快车系列答案【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.
(1)根据题意,填写下表:
快递物品重量(千克) | 0.5 | 1 | 3 | 4 | … |
甲公司收费(元) | 22 | … | |||
乙公司收费(元) | 11 | 51 | 67 | … |
(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.