题目内容
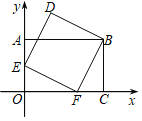
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF相交于点O,下列结论:
①∠DOC=90°,②OC=OE,③tan∠OCD=![]() ,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
,④△COD的面积等于四边形BEOF的面积,正确的有 ( )
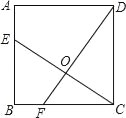
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:
由已知条件证△EBC≌△FCD,从而可得∠BCE=∠FDC,结合∠BCE+∠OCD=90°可得∠FDC+∠OCD=90°,由此可得∠DOC=90°,即可得到结论①正确;再证∠OCD=∠DFC可推导得到结论③正确;由△EBC≌△FCD推导可得结论④正确;连接DE,假设结论②成立可推导得到DE=DC=DA,这与DE>DA矛盾,从而说明结论②错误;
详解:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=4,∠A=∠B=∠BCD=90°,
∵AE=BF=1,
∴AB-AE=BC-BF=4-1=3,即BE=CF=3,
∴△EBC≌△FCD,tan∠DFC=![]() ,
,
∴∠BCE=∠FDC,
∵∠BCE+∠OCD=90°,
∴∠FDC+∠OCD=90°,
∴∠DOC=180°-90°=90°,即结论①正确;
∴∠FOC=90°,
∴∠OFC+∠OCF=90°,
∵∠OCF+∠OCD=90°,
∴∠OCD=∠OCF,
∴tan∠OCD= tan∠DFC=![]() ,即结论③正确;
,即结论③正确;
∵△EBC≌△FCD,
∴S△EBC-S△FOC=S△FCD-S△FOC,
∴S四边形BEOF=S△OCD,即结论④正确;
如下图,连接DE,假设②OC=OE成立 ,
∵∠DOC=90°,
∴DF垂直平分AC,
∴DE=DC,
∵DC=DA,
∴DE=DA,而这与Rt△ADE中,直角边AD小于斜边DE矛盾,
∴结论②错误,

综上所述,正确的结论是①③④共3个.
故选C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】用火柴按下图中的方式搭图形:

(1)按图示规律补全表格:
图形编号 | ① | ② | ③ | ④ | ⑤ |
火柴棒根数 | 7 | 12 |
|
|
|
(2)按照这种方式搭下去,请写出搭第n个图形需要的火柴根数;
(3)小明发现:按照这种方式搭图形会产生若干个正方形,若使用187根火柴搭图形,图中会产生多少个正方形?
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元,设小明快递物品x千克.
(1)根据题意,填写下表:
快递物品重量(千克) | 0.5 | 1 | 3 | 4 | … |
甲公司收费(元) | 22 | … | |||
乙公司收费(元) | 11 | 51 | 67 | … |
(2)设甲快递公司收费y1元,乙快递公司收费y2元,分别写出y1,y2关于x的函数关系式;
(3)当x>3时,小明应选择哪家快递公司更省钱?请说明理由.