题目内容
【题目】解决下列两个问题:
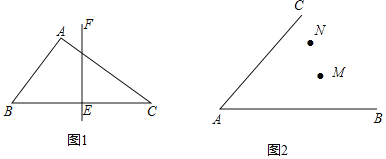
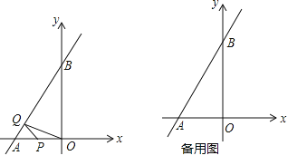
(1)如图1,在△ABC中,AB=3,AC=4,BC=5.EF垂直且平分BC.点P在直线EF上,直接写出PA+PB的最小值,并在图中标出当PA+PB取最小值时点P的位置;
解:PA+PB的最小值为 .
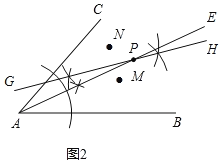
(2)如图2.点M、N在∠BAC的内部,请在∠BAC的内部求作一点P,使得点P到∠BAC两边的距离相等,且使PM=PN.(尺规作图,保留作图痕迹,无需证明)
【答案】(1)4;(2)见解析
【解析】
(1)根据题意知点B关于直线EF的对称点为点C,故当点P与点D重合时,AP+BP的最小值,求出AC长度即可得到结论.
(2)作∠AOB的平分线OE,作线段MN的垂直平分线GH,GH交OE于点P,点P即为所求.
(1)点P的位置如图所示:
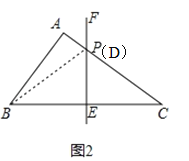
∵EF垂直平分BC,∴B、C关于EF对称,设AC交EF于D,∴当P和D重合时,AP+BP的值最小,最小值等于AC的长,即最小值为4.
故答案为:4.
(2)如图,①作∠AOB的平分线OE,②作线段MN的垂直平分线GH,GH交OE于点P,则点P即为所求.

练习册系列答案
相关题目