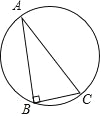题目内容
【题目】如图1,在 ![]() 中,
中, ![]() ,AC=BC,
,AC=BC, ![]() ,
, ![]() ,垂足分别为D,E.
,垂足分别为D,E.
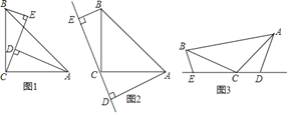
(1)若AD=2.5cm,DE=1.7cm,求BE的长.
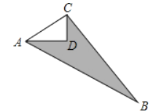
(2)如图2,在原题其他条件不变的前提下,将CE所在直线旋转到 ![]() ABC的外部,请你猜想AD,DE,BE三者之间的数量关系,直接写出结论:________.(不需证明)
ABC的外部,请你猜想AD,DE,BE三者之间的数量关系,直接写出结论:________.(不需证明)
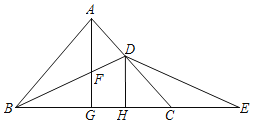
(3)如图3,若将原题中的条件改为:“在 ![]() ABC中,AC=BC,D,C,E三点在同一条直线上,并且有
ABC中,AC=BC,D,C,E三点在同一条直线上,并且有 ![]() ,其中
,其中 ![]() 为任意钝角”,那么(2)中你的猜想是否还成立?若成立,请予以证明;若不成立,请说明理由.
为任意钝角”,那么(2)中你的猜想是否还成立?若成立,请予以证明;若不成立,请说明理由.
【答案】(1)BE=0.8cm;(2)AD+BE=DE;(3)成立,证明详见解析.
【解析】
(1)利用垂直的定义及同角的余角相等,可证得∠EBC=∠DCA,利用AAS可证得△CEB≌△ADC,再利用全等三角形的对应边相等,可证得BE=CD,CE=AD,从而可求出DC的长,即可得到BE的长.
(2)利用垂直的定义及同角的余角相等,可证得∠EBC=∠DCA,利用AAS可证得△CEB≌△ADC,再利用全等三角形的对应边相等,可证得BE=CD,CE=AD,然后根据DE=CE+DE,即可证得结论.
(3)利用同样的方法,可证得BE=CD,CE=AD,然后根据DE=EC+CD,即可得到DE,AD,BE之间的数量关系.
(1)解:∵ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
在 ![]() 和
和 ![]() 中,
中,
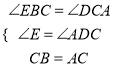 ,
,
![]() ,
,
![]()
∵DC=CE-DE,DE=1.7cm,
∴BE=0.8cm
(2)AD+BE=DE,(不需证明)理由如下:
证明:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中,
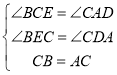 ,
,
∴△CEB≌△ADC(AAS),
∴BE=DC,CE=AD,
∴DE=CE+DE=AD+BE
(3)(2)中的猜想还成立,
证明:∵ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]()
在 ![]() 和
和 ![]() 中,
中,
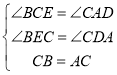 ,
,
![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]()

 导学教程高中新课标系列答案
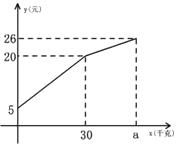
导学教程高中新课标系列答案【题目】某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收1元印刷费,另收150元的制版费;乙印刷厂提出:每份材料收2.5元印刷费,不收制版费.设在同一家印刷厂一次印制数量为![]() 份(
份(![]() 为正整数).
为正整数).
(1)根据题意,填写下表:
一次印制数量(份) | 5 | 10 | 20 | … |
|
甲印刷厂收费(元) | 155 | … | |||
乙印刷厂收费(元) | 12.5 | … |
(2)在印刷品数量大于800份的情况下选哪家印刷厂印制省钱?