题目内容
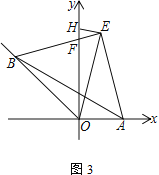
【题目】如图,一次函数y=x+3的图象与x轴,y轴交于A,B两点,与反比例函数 ![]() 的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
①△CEF与△DEF的面积相等;
②△AOB∽△FOE;
③△DCE≌△CDF;
④AC=BD.
其中正确的结论是( )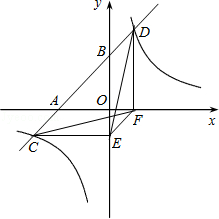
A.①②
B.①②③
C.①②③④
D.②③④
【答案】C
【解析】解:①设D(x, ![]() ),则F(x,0),
),则F(x,0),
由图象可知x>0,
∴△DEF的面积是: ![]() ×|
×| ![]() |×|x|=2,
|×|x|=2,
设C(a, ![]() ),则E(0,
),则E(0, ![]() ),
),
由图象可知: ![]() <0,a>0,
<0,a>0,
△CEF的面积是: ![]() ×|a|×|
×|a|×| ![]() |=2,
|=2,
∴△CEF的面积=△DEF的面积,
故①正确;②△CEF和△DEF以EF为底,则两三角形EF边上的高相等,
故EF∥CD,
∴FE∥AB,
∴△AOB∽△FOE,
故②正确;③∵C、D是一次函数y=x+3的图象与反比例函数 ![]() 的图象的交点,
的图象的交点,
∴x+3= ![]() ,
,
解得:x=﹣4或1,
经检验:x=﹣4或1都是原分式方程的解,
∴D(1,4),C(﹣4,﹣1),
∴DF=4,CE=4,
∵一次函数y=x+3的图象与x轴,y轴交于A,B两点,
∴A(﹣3,0),B(0,3),
∴∠ABO=∠BAO=45°,
∵DF∥BO,AO∥CE,
∴∠BCE=∠BAO=45°,∠FDA=∠OBA=45°,
∴∠DCE=∠FDA=45°,
在△DCE和△CDF中 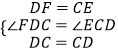 ,
,
∴△DCE≌△CDF(SAS),
故③正确;④∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,
故④正确;
正确的有4个.
故选:C.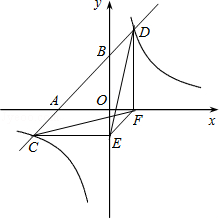
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.

 名校课堂系列答案
名校课堂系列答案