Question

【题目】如图，已知直线l经过点A(－1,0)和点B(1,4)．

（1）求直线l的解析式；

（2）若点P是x轴上的点，且△APB的面积为8，求点P的坐标．

Answer 1

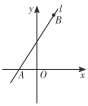
【答案】（1）y＝2x＋2；（2）P (－5，0)或(3，0)．

【解析】

（1）首先设出设直线l1的解析式为y=kx+b（k≠0），根据待定系数法把点A（-1，0）和点B（1，4）代入设的解析式，即可求出一次函数的解析式；

（2）根据三角形的面积计算出AP的长，进而得到P点坐标．

（1）设直线l1的解析式为y=kx+b（k≠0），

∵一次函数的图象经过点A（-1，0）和点B（1，4），

∴，

解得，

∴直线l1的解析式为y=2x+2；

（2）∵△APB的面积为8，点B（1，4），

∴×AP×4=8，

解得：AP=4，

∵点A（-1，0），

∴P（-5，0）或（3，0）．