题目内容
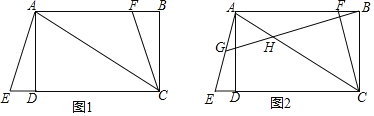
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE.F为AB上的一点,且BF=DE,连接FC.
(1)若DE=1,CF=![]() ,求CD的长;
,求CD的长;
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=![]() AC.
AC.
【答案】(1)CD=3;(2)见解析.
【解析】
(1)根据矩形的性质先由勾股定理求得BC的值再通过AC2=AD2+CD2即可求得CD的长;
(2)如图2中,连接CG.作FJ⊥AC于J.通过证明∠BAC=30°,∠ACF=45°即可解决问题.
(1)设CD=x.
∵四边形ABCD是矩形,
∴∠ADC=∠B=90°,AD=BC,
在Rt△BCF中,BC=![]() ,
,
∵AC=CE=x+1,
在Rt△ADC中,∵AC2=AD2+CD2,
∴![]() ,
,
∴x=3,
∴CD=3;
(2)如图2中,连接CG.作FJ⊥AC于J.

∵CA=CE,AG=EG,
∴CG⊥AE,∠ACG=∠ECG,
∵∠AGC=∠ABC=90°,
∴∠AGC+∠ABC=180°,
∴A、G、C、B四点共圆,
∴∠ABG=∠ACG,
∴∠ACG=∠ECG=∠ABG,设∠ACG=∠ECG=∠ABG=x,则∠BAH=∠ACD=2x,∠BHC=∠BAH+∠ABG=3x,
∵∠BHC+∠ABG=60°,
∴4x=60°,
∴x=15°,
∴∠FAJ=30°,∠DAC=∠ACB=60°,∠CAE=75°,
∴∠EAD=15°,
∵DE=BF,∠ADE=∠CBF,AD=BC,
∴![]() ,
,
∴∠BCF=∠DAE=15°,
∴∠FCJ=45°,
∴CJ=FJ,设CJ=FJ=a,则AJ=![]() ,AF=2a,AC=
,AF=2a,AC=![]() ,
,
∴![]() ,
,
∴AF=![]() ,
,
∴AF=![]() ,∵AC=CE,
,∵AC=CE,
∴![]() .
.

练习册系列答案
相关题目