题目内容
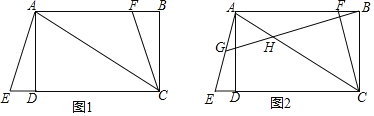
【题目】某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:
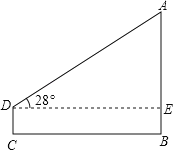
方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹杆的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度(精确到0.1米)若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度(结果可用字母表示)
【答案】可行,旗杆高度约为22.9米.
【解析】
方法1:在直角三角形AED中,利用BC的长和已知的角的度数,利用正切函数可求得AB的长.
方法2:根据物高与影长的关系,将实际问题转化为数学问题.
解:方法1:由题意则DE=BC,即DE=40米.
在直角△ADE中,∠ADE=28°,
AE=DEtan28°=40tan28°(米).
则AB=AE+EB=40tan28°+1.6(米).
答:旗杆高度为(40tan28°+1.6)米.
方法2:∵物高与影长成比例,
∴旗杆的高度:17.15=2:1.5,
∴旗杆的高度=34.3÷1.5≈22.9米.
答:旗杆高度约为22.9米.


练习册系列答案
相关题目
【题目】东坡商贸公司购进某种水果成本为20元/![]() ,经过市场调研发现,这种水果在未来48天的销售单价
,经过市场调研发现,这种水果在未来48天的销售单价![]() (元/
(元/![]() )与时间
)与时间![]() (天)之间的函数关系式
(天)之间的函数关系式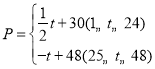 ,
,![]() 为整数,且其日销售量
为整数,且其日销售量![]() (
(![]() )与时间
)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | … |
日销售量 | 118 | 114 | 108 | 100 | 80 | … |
(1)已知![]() 与
与![]() 之间的变化符合一次函数关系,试求在第30天的日销售量;
之间的变化符合一次函数关系,试求在第30天的日销售量;
(2)哪一天的销售利润最大?最大日销售利润为多少?