题目内容
如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.
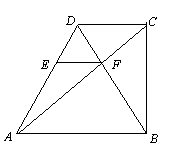
⑴求证:四边形ABFE是等腰梯形;
⑵求AE的长.

⑴求证:四边形ABFE是等腰梯形;
⑵求AE的长.
⑴证明略;⑵AE=BF=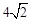 .
.
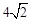 .
.(1)过点D作DM⊥AB,根据已知可求得四边形BCDM为矩形,从而得到DC=MB,因为AB=2DC,从而推出△ABD是等腰三角形,从而得到∠DAB=∠DBA,因为EF∥AB,AE不平行FB,所以AEFB为梯形,从而根据同一底上的两个角相等的梯形是等腰梯形得证;
(2)由已知可得到△DCF∽△BAF,根据相似三角形的对应边成比例,可得到AF的长,再根据△BCF∽△ACB,得到BF2=CF•AF,从而求得BF的长,由第一问已证得BF=AE,所以就求得了AE的长
(2)由已知可得到△DCF∽△BAF,根据相似三角形的对应边成比例,可得到AF的长,再根据△BCF∽△ACB,得到BF2=CF•AF,从而求得BF的长,由第一问已证得BF=AE,所以就求得了AE的长

练习册系列答案
相关题目

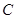 将线段
将线段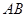 分成两部分,如果
分成两部分,如果 ,那么称点
,那么称点 将一个面积为
将一个面积为 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为 ,
, ,如果
,如果 ,那么称直线
,那么称直线
 中,若点
中,若点 为
为 是
是 ,再过点
,再过点 ,交
,交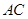 于点
于点 ,连接
,连接 (如图3),则直线
(如图3),则直线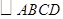 的边
的边 ,交
,交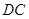 于点
于点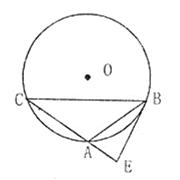
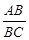 =
=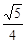 时,①求tan∠ABE的值;②如果AE=
时,①求tan∠ABE的值;②如果AE=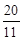 ,求AC的值。
,求AC的值。
 (3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P
(3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P
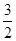 ,则△A′B′C′的面积是________________.
,则△A′B′C′的面积是________________.
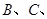
 三个食品加工厂,这三个工厂和开发区
三个食品加工厂,这三个工厂和开发区 处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且
处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且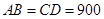 米,
米, 米.自来水公司已经修好一条自来水主管道
米.自来水公司已经修好一条自来水主管道 两厂之间的公路与自来水管道交于
两厂之间的公路与自来水管道交于 处,
处, 米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
